Ángulo
En geometría , la noción general de ángulo se puede dividir en varios conceptos.
En su sentido antiguo, el ángulo es una figura plana, una porción del plano delimitada por dos medias líneas . Así es como hablamos de los ángulos de un polígono . Sin embargo, ahora se acostumbra utilizar el término "sector angular" para tal figura. El ángulo también puede designar una porción del espacio delimitada por dos planos ( ángulo diedro ). La medición de tales ángulos también se llama comúnmente, pero incorrectamente, ángulo.
En un sentido más abstracto, el ángulo es una clase de equivalencia , es decir, un conjunto obtenido asimilando entre sí todas las figuras angulares identificables por isometría . Cualquiera de las figuras identificadas se denomina representante del ángulo. Teniendo todos estos representantes la misma medida, podemos hablar de una medida del ángulo abstracto.
Es posible definir una noción de ángulo orientado en la geometría euclidiana del plano, así como extender la noción de ángulo al marco de los espacios vectoriales prehilbertianos o variedades de Riemann .
Hay varios tipos de ángulos: ángulo recto , ángulo agudo y ángulo obtuso.
Historia
La palabra ángulo deriva del latín angulus , una palabra que significa "la esquina". Según el matemático Carpos de Antioquía , el ángulo es una cantidad y el intervalo de las líneas o superficies que lo incluyen; este espacio se dimensiona de una manera y, sin embargo, el ángulo no es una línea para él.
El ángulo como figura del plano o del espacio.
Ángulo y sector angular
En el plano, dos semilíneas del mismo origen delimitan dos regiones, llamadas sectores angulares .
Decimos que dos sectores angulares definen el mismo ángulo cuando son superponibles (más formalmente: el ángulo de un sector angular es su clase de congruencia ). Tradicionalmente hablamos de ángulo geométrico para esta noción de ángulo, pero este término también puede designar, en terminología moderna, una noción similar menos fina ( ver más abajo ).
Se dice que un ángulo es sobresaliente si los sectores angulares que lo representan son convexos y reentrantes si no.
Por tanto, un par de semilíneas del mismo origen define generalmente dos ángulos: uno saliente y otro reentrante (el caso excepcional es el del ángulo plano ).
En el plano, podemos hablar del ángulo de dos rectas que se cruzan. Dos líneas secantes cortan el plano en 4 sectores angulares salientes, correspondientes a dos pares de ángulos opuestos por el vértice. Los ángulos opuestos son iguales y los ángulos adyacentes son adicionales . Generalmente hay dos valores posibles para estos ángulos. A veces optamos por favorecer el ángulo más pequeño, es decir, el ángulo agudo o recto.
Valor de ángulo
La medida del ángulo de un sector angular es el número real positivo que mide la proporción del plano ocupado por el sector angular. Las unidades utilizadas para cuantificarlo son el radianes , el cuadrante y sus subdivisiones, el grado , sus subunidades y el grado . Los ángulos se denotan frecuentemente con una letra griega minúscula, por ejemplo α, β, θ, ρ ... Cuando el ángulo está en la parte superior de un polígono y no hay ambigüedad, entonces se usa el nombre de la parte superior coronada por un sombrero, por ejemplo  .
Para evaluar este ángulo, esta "proporción de superficie", tomamos un disco centrado en el punto de intersección, y calculamos la relación entre el área de la porción del disco interceptada por el sector angular y el área total del disco. . Podemos mostrar que esto también equivale a establecer la relación entre la longitud del arco interceptado y la circunferencia del círculo; este valor menor que 1 se llama número de vueltas . El valor 1/4 (cuarto de vuelta) corresponde al cuadrante .
Una unidad de uso común es el grado , que es el resultado de dividir el cuadrante en 90 partes iguales. Por tanto, el giro completo corresponde a 360 grados. El minuto de arco es un submúltiplo de un grado, igual a 1/60 de un grado. Asimismo, el segundo de arco es igual a 1/60 del minuto de arco, o 1/3600 de grado. El grado se usa con menos frecuencia , que corresponde a una subdivisión centesimal del cuadrante.
Sin embargo, la unidad internacional de medida de los ángulos es el radián , definido como la relación entre la longitud del arco interceptado y el radio del círculo. Por tanto, la revolución completa corresponde a radianes.
Los ángulos se pueden calcular a partir de las longitudes de los lados de los polígonos , especialmente los triángulos , mediante trigonometría .
La unidad de medida de los ángulos utilizada principalmente por los militares es la milésima . Es el ángulo en el que vemos de 1 metro a 1 kilómetro. 6283 milésimas corresponde a 2π radianes o 360 grados, o 360 ° / arctan (1 m / 1000 m ). En otras palabras, milésima = mrad (milirradian).
Los ángulos "en el campo" se pueden medir con un dispositivo llamado goniómetro ; generalmente comprende una regla curva graduada en grados, llamada transportador .
En informática, se puede utilizar 1/16 de grado, o 5760 para 360 °.
Nombre de los ángulos
Los ángulos correspondientes a un número entero de cuadrantes tienen un nombre especial. La siguiente tabla representa los valores de los ángulos particulares en las distintas unidades.
| Ángulo | Representación | Número de vueltas | Numero de cuadrantes | Radianes | La licenciatura | Calificación |
|---|---|---|---|---|---|---|
| Ángulo completo | 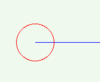 |
1 turno | 4 cuadrantes | 2π rad | 360 ° | 400 gr |
| Ángulo plano |  |
1/2 vuelta | 2 cuadrantes | π rad | 180 ° | 200 gr |
| Ángulo recto |  |
1/4 de vuelta | 1 cuadrante | π / 2 rad | 90 ° | 100 gr |
| Ángulo cero | 0 ronda | 0 cuadrante | 0 rad | 0 ° | 0 gr |
El ángulo recto se obtiene considerando dos líneas que dividen el plano en cuatro sectores iguales. Se dice que tales líneas son ortogonales o perpendiculares.
El ángulo se confunde con frecuencia con su medida. Así, por ejemplo, se dice erróneamente que un ángulo plano es "igual" a 180 °. Este abuso se practica ampliamente en el resto de este artículo.
Los siguientes calificadores se utilizan para ángulos que toman valores intermedios entre estos valores notables:
- el ángulo de reentrada es un ángulo mayor que el ángulo plano;
- el ángulo saliente es un ángulo menor que el ángulo plano:
- el ángulo obtuso está entre 90 ° y 180 °,
- el ángulo agudo está entre 0 ° y 90 °.
Para calificar los valores relativos de dos ángulos, usamos las siguientes expresiones:
- dos ángulos son complementarios cuando su suma es de 90 ° ; si dos ángulos son complementarios, se dice que cada uno es el complemento del otro;
- dos ángulos son adicionales cuando su suma es 180 ° .
Todavía usamos otras expresiones para calificar la posición de los ángulos en una figura, es decir, más precisamente, la posición relativa de los sectores angulares:
- dos sectores angulares son opuestos en la parte superior, cuando tienen la misma parte superior y los lados de uno son una extensión de los del otro. En este caso, los ángulos correspondientes son iguales.
- dos sectores angulares son adyacentes cuando tienen el mismo vértice, un lado común y su intersección es igual a este lado común. Los ángulos se suman al considerar la unión de estos sectores.
- los ángulos alternos-externos y los alternos-internos están formados por dos líneas rectas cortadas por una secante . Estos ángulos tienen la misma medida cuando las dos líneas son paralelas.
Nota, dos ángulos complementarios o adicionales no son necesariamente adyacentes: Por ejemplo, en una derecha en ángulo ABE triángulo en B, los ángulos A y E son complementarios.
Por extensión, también definimos los ángulos entre medias líneas, segmentos de línea y vectores , extendiendo las líneas que llevan estos objetos hasta su intersección. La definición por medias líneas o vectores permite eliminar la indeterminación entre los ángulos adicionales, es decir, definir sin ambigüedad qué sector angular utilizar para definir la inclinación de las direcciones.
Ángulo geométrico
Un ángulo geométrico es, en la terminología actual, la clase de equivalencia de un par de medias líneas del mismo origen, considerándose equivalentes dos de estos pares si son superponibles .
Si se observa el ángulo geométrico asociado al par de semilíneas , se tiene (por simetría con respecto a la bisectriz ) :, es decir que este ángulo depende únicamente del par .
El ángulo saliente y el ángulo reentrante asociados con dicho par ( ver arriba ) corresponden, por lo tanto, con esta nueva terminología, al mismo "ángulo geométrico", cuyo representante preferido es el ángulo saliente (medido entre 0 y 180 ° ).
Se puede interpretar de varias formas: divergencia entre dos direcciones, direcciones de las caras de un objeto (esquina), dirección en relación al norte (ángulo dado por una brújula) ... El ángulo también se puede interpretar como la apertura del sector angular. Es la medida de la inclinación de una media línea en relación con la otra.
Si una traducción transforma en y en , no cambia el ángulo geométrica: . Por tanto, podemos definir el ángulo geométrico de dos vectores distintos de cero y como el ángulo entre dos medias líneas dirigidas por estos dos vectores, y de origen común arbitrario. O de nuevo: dos pares y vectores distintos de cero son equivalentes (representan el mismo ángulo geométrico) si hay una isometría vectorial que transforma los vectores unitarios y en y . (Por tanto, definimos una relación de equivalencia entre parejas, porque las isometrías vectoriales forman un grupo ).
Ángulos orientados en el plano
Un enfoque múltiple
La presentación de ángulos orientados en un plano se puede realizar de forma intuitiva o más formalista.
El primer enfoque consiste en ver el ángulo como el rastro de una rotación: la rotación que envía la media línea (Buey) sobre la media línea (Oy) es en general diferente de la que envía (Oy) sobre (Ox). Los ángulos (Ox, Oy) y (Oy, Ox) se consideran distintos, lo que indica que tienen la misma medida pero diferentes direcciones de viaje.
Otro enfoque consiste en confundir el ángulo orientado y su medida. Este enfoque requiere definir una orientación previa del plan para poder definir el llamado significado positivo . Es este tipo de enfoque el que encontramos cuando definimos la medida del ángulo orientado de un par de vectores unitarios usando la longitud del arco circular orientado que determina en un círculo unitario.
El último enfoque, más formalizado, consiste en ver un ángulo orientado como una clase de equivalencia de pares de semilíneas vectoriales módulo las rotaciones del plano, o lo que equivale a lo mismo, como órbitas de pares de semilíneas vectoriales por la acción grupal de isometrías positivas.
Posteriormente, se presentarán los enfoques por las longitudes de arcos de círculos y como clases de equivalencia. Usando las mismas técnicas que arriba, equivale a lo mismo, cuando se habla de ángulos, considerar dos medias líneas del mismo origen, dos vectores distintos de cero o dos vectores unitarios. Por lo tanto, limitamos la discusión al último caso.
Arcos circulares orientados
En un círculo con centro O y radio 1, definimos una dirección de desplazamiento denominada positiva , en general la dirección contraria a las agujas del reloj, denominada dirección trigonométrica. Si A y B son dos puntos del círculo, llamamos longitud del arco orientado AB, la longitud de cualquier ruta en el círculo que comienza en A y llega a B. Hay varias rutas posibles que consisten en sumar giros completos del círculo recorrido. en la dirección positiva o en la dirección negativa. Una longitud de un ser conocido, las otras longitudes de los arco orientadas son por lo tanto, todo de la forma de un + 2 k π donde k es cualquier entero relativo. La longitud correspondiente al camino más corto para ir de A a B se denomina medida principal del arco AB (si hay dos caminos posibles, se elige el de medida positiva). Por tanto, la medida principal es un número que pertenece al intervalo] -π, π].
Sean y dos vectores unitarios, y A y B los puntos tales que y , llamamos a la medida del ángulo orientado cualquier longitud del arco orientado AB. Por tanto, la medida principal del ángulo tiene como valor absoluto la medida del ángulo geométrico . El signo de esta medida principal es positivo si el camino más corto de A a B está en la dirección directa, de lo contrario es negativo. Dos pares de vectores que tienen la misma medida definen el mismo ángulo orientado.
En este planteamiento, es necesario que el “enrollamiento” de la recta real sobre el círculo sea percibido como natural, un enrollamiento que queda por formalizar.
Ángulos dirigidos de vectores por clase de equivalencia
El plano tiene la siguiente peculiaridad, en comparación con las dimensiones superiores: podemos afinar la relación de congruencia definida para el ángulo geométrico de tal manera que los pares y no representen el mismo ángulo en general. Para ello, se evita involucrar las reflexiones entre las isometrías autorizadas para definir una nueva relación entre las parejas, es decir que se limita al subgrupo de las rotaciones del plano vectorial (en la dimensión 3 por ejemplo, esta limitación fallaría porque las dos parejas se transforman entre sí no solo por reflexión con respecto al plano bisector, sino también por una rotación de media vuelta). Esto lleva a la siguiente definición:
Un ángulo orientado de vectores es una clase de equivalencia(Ahora prescindimos de las flechas tradicionales en los vectores).
Dos pares (u, v) y (u ', v') de vectores unitarios del plano representan el mismo ángulo orientado si hay una rotación g tal que u '= g (u) y v' = g (v).
Al confundir incorrectamente un par y el ángulo orientado que representa, tenemos, por ejemplo: (–u, –v) = (u, v) por la media vuelta g = - Id .
Esta nueva relación de equivalencia es más fina que la que define los ángulos geométricos. Más precisamente, como clase de equivalencia, el ángulo geométrico es la unión de los dos ángulos orientados y .
Cada ángulo orientado corresponde a una rotaciónDados dos vectores unitarios, hay una sola rotación del plano que envía el primero al segundo.
Esta unicidad permite definir una aplicación que al par (u, v) de vectores unitarios asocia la rotación f tal que f (u) = v.
Este mapa T: (u, v) ↦ f, de los pares de vectores a las rotaciones, “ pasa al cociente ”, y así define una biyección S, desde los ángulos dirigidos hacia las rotaciones. En efecto :
Teorema - (u, v) y (u ', v') representan el mismo ángulo orientado si y solo si la rotación que envía u sobre v es la misma que envía u 'sobre v'.
Esto se debe al hecho de que el grupo de rotaciones del plano vectorial es abeliano .
DemostraciónPor definición, (u, v) y (u ', v') representan el mismo ángulo orientado si y solo si la rotación que envía u sobre u 'es la misma que envía v sobre v', en otras palabras: T (u, u ') = T (v, v'). Por conmutatividad del grupo de rotaciones, esto es equivalente a T (u ', v) ∘T (u, u') = T (v, v ') ∘T (u', v), es decir T (u, v) = T (u ', v').
Los ángulos orientados de los vectores forman un grupoUsando esta biyección S, podemos entonces "mapear" la estructura de grupo abeliano (en) del grupo de rotaciones sobre el conjunto de ángulos, es decir definir la suma de los ángulos a partir de la composición de las rotaciones, estableciendo:
.- Con esta adición, los ángulos orientados de los vectores forman un grupo abeliano.
- Con T (u, v) ∘ T (v, w) = T (u, w), obtenemos para los ángulos la relación de Chasles (u, v) + (v, w) = (u, w).
- El ángulo cero corresponde a la identidad: (u, u) = 0.
- (v, u) + (u, v) = (v, v) = 0 y por lo tanto (v, u) es el opuesto de (u, v) (ver figura anterior).
-
Cualquier ángulo es divisible por n de n maneras. Por ejemplo, para n = 2:
- los dos ángulos cuyo doble es el ángulo cero (u, u) son el ángulo plano (u, –u) y el ángulo cero;
- hay dos ángulos rectos, soluciones de 2 (u, v) = (u, –u).
- Las isometrías directas (rotaciones) conservan los ángulos orientados de los vectores, por definición.
- Las isometrías indirectas (reflexiones) transforman cualquier ángulo orientado de los vectores en el ángulo opuesto porque para cualquier línea D, un ángulo siempre puede ser representado por un par (u, v) de los cuales D es la bisectriz, y la reflexión del eje D luego intercambia u y V.
Definiremos, sobre los ángulos orientados, una medida, de tal manera que la medida de la suma sea igual a la suma de las medidas (para ángulos geométricos, podríamos definir parcialmente una suma de los ángulos y las medidas correspondientes: solo para ángulos "no demasiado grandes").
La elección de una de las dos posibles orientaciones del plano determina uno de los dos isomorfismos del grupo de rotaciones con el grupo SO (2) de las matrices de rotaciones planas o con el grupo U de los números complejos de módulo 1 . El exponencial complejo hace posible definir la medida del ángulo de una rotación dentro de 2π , o "módulo 2π" (en radianes). Si θ es una medida del ángulo de rotación f = T (u, v), diremos que θ también es una medida del ángulo orientado de los vectores (u, v).
Por ejemplo, se anota la medida del ángulo recto de dirección directa:
o bien
.En resumen, una orientación del plano que se elige, la medida de un ángulo orientado de vectores se define por:
,donde la matriz es la de T (u, v) en cualquier base ortonormal directa .
Es un isomorfismo del grupo de ángulos orientados en el grupo aditivo de “módulo real 2π” . Por tanto, la medida de ángulos es finalmente aditiva.
Sin embargo, recuerde que depende de la elección de la orientación de la toma : invertir esta elección cambia todos los compases en sus opuestos . Encontramos aquí el hecho de que un ángulo geométrico, de medida α entre 0 y π, corresponde a dos ángulos orientados opuestos, siendo la atribución (módulo 2π) de la medida α a uno y por tanto –α al otro en función de la orientación del avión.
Además, Daniel Perrin y Jean Dieudonné señalan que no podemos hablar estrictamente de medición porque no es posible realizar una comparación entre dos mediciones de ángulos.
Ángulo orientado de dos líneas
En un plano, el ángulo orientado de dos líneas es la clase módulo π del ángulo orientado formado por sus vectores de dirección. Este trabajo de módulo π proviene del hecho de que podemos tomar como vector director de una línea recta u o -u y que cambiar un vector en su opuesto equivale a sumar π a la medida del ángulo correspondiente.
Los ángulos orientados a la línea se utilizan para determinar el ángulo de una rotación formada por dos reflejos. Esta noción también es útil para todos los problemas de alineación y ciclicidad.
Ángulos en el espacio
Dos rectas que se cruzan son necesariamente coplanares, por lo que el ángulo entre las rectas se define en este plano, de la misma forma que arriba.
En el espacio, no existe la noción de un ángulo de líneas orientado, pero podemos definir el ángulo de dos líneas cualesquiera en el espacio, secantes o no, a condición de trabajar en sus vectores de dirección. El ángulo de dos líneas se llama ángulo geométrico formado por sus vectores de dirección. Generalmente hay dos valores posibles para este ángulo, dependiendo de los vectores de dirección elegidos. A veces se prefiere el ángulo más pequeño. Por lo tanto, el ángulo entre dos líneas paralelas es cero y el ángulo entre dos líneas ortogonales es de 90 ° o π / 2 rad.
El ángulo de dos líneas de vectores de dirección uyv se puede determinar usando el producto escalar: es el ángulo cuyo coseno es igual .
También podemos considerar la noción vecina de ángulo de dos ejes, en la que la orientación de los ejes impone un valor único al ángulo que forman.
Para definir el ángulo entre dos planos, o ángulo diedro , consideramos el ángulo formado por sus normales .
Para definir el ángulo entre un plano y una recta, consideramos el ángulo α entre la recta y su proyección ortogonal en el plano, o el ángulo complementario entre la recta y la normal al plano: restamos el ángulo β entre la recta y la normal al plano del ángulo recto (α = π / 2 - β en radianes).
También definimos los ángulos sólidos : tomamos un punto (a veces llamado "punto de observación") y una superficie en el espacio (la "superficie observada"), el ángulo sólido es la porción del espacio delimitada por el cono que tiene como vértice el punto considerado y descansando sobre el contorno de la superficie. El ángulo sólido se mide calculando el área de la tapa cortada por el cono en la esfera de radio uno y centrando el vértice del cono. La unidad de medida para el ángulo sólido es el estereorradián (sr para abreviar), el espacio completo es 4π sr.
Uso de ángulos
- En geodesia ( geografía ):
- acimut : ángulo con respecto al eje norte-sur en un plano que contiene este eje y el punto de destino, contado en relación con el norte contado en el sentido de las agujas del reloj;
- latitud : ángulo formado por una vertical que parte de un punto y va hacia el centro de la Tierra en relación con el plano del ecuador; los puntos que tienen la misma latitud forman un círculo llamado "paralelo";
- longitud : ángulo que permite ubicarse en la Tierra: ángulo formado por el plano que contiene el eje Norte-Sur y el punto considerado, denominado "plano meridiano", con un plano de referencia que también contiene el eje Norte-Sur; la intersección de un plano meridiano con la superficie de la Tierra es un semicírculo llamado meridiano . El meridiano de referencia es el " meridiano de Greenwich ";
- línea de altura : posición de un punto calculado, incluido el acimut y la diferencia angular, con respecto a un punto estimado;
- pendiente : tangente del ángulo de un terreno con respecto a la horizontal.
- En astronomía :
- acimut (o acimut): cuando se apunta a un punto desde el centro de la Tierra, ángulo con respecto al eje Norte-Sur en un plano que contiene este eje y el punto objetivo, contado con respecto al Sur;
- diámetro aparente : ángulo en el que vemos un objeto o una estrella;
- distancia cenital : ángulo entre la vertical y el punto de destino;
- altura : ángulo entre la horizontal y el punto de destino;
- inclinación : ángulo entre el plano de la órbita de un cuerpo celeste y el plano de referencia;
- paralaje : ángulo formado por la mirada de una persona que fija cualquier punto de un objeto y su cambio de posición;
- nadir : ángulo recto hacia abajo verticalmente al horizonte del observador;
- cenit : ángulo recto hacia arriba verticalmente al horizonte del observador.
- En óptica geométrica :
- ángulo de incidencia: ángulo entre un vector y el vector de la superficie, por ejemplo en reflexión y en refracción , ángulo entre un rayo de luz y la normal a la superficie de una dioptría;
- paralaje .
- En aerodinámica :
- En balística :
- seguridad
Notas y referencias
- Matemáticas , CEPL, coll. "Enciclopedias del conocimiento moderno",1975( leer en línea ) , pág. 154.
- Nadine Jacob, Claude Courivaud, Matemáticas. En tercer lugar , Brevet Sequence, Bréal, pág. 200
- Dany-Jack Mercier, Actualización de AGA: Revisión equilibrada de temas de álgebra, geometría y aritmética , vol. 1,2011( leer en línea ) , pág. 242.
- Matemáticas CRPE , vol. 2, Dunod,2017( leer en línea ) , pág. 51.
- Michèle Audin , Geometría ( L3 M1) , Les Ulis, Ciencias EDP ,2006, 3 e ed. , 420 p. ( ISBN 978-2-86883-883-4 , aviso BnF n o FRBNF40151336 , leer en línea ) , p. 79-80.
- Esta presentación es la que se encuentra, por ejemplo, en la enseñanza de francés en cuarta clase en 1988 IREM de Estrasburgo, Matemáticas - 4º -collectinn Istra, p. 236)
- Este es el enfoque propuesto por Daniel Perrin en A propos d'angles orientadas , p.2.
- Esta presentación es la que encontramos por ejemplo en la enseñanza del francés en segundo grado en 1994 (Colección Terracher, Math - Seconde - Hachette education, p. 189)
- Marcel Berger, Géométrie T.2 Espacios euclidianos, triángulos, círculos y esferas, Cedic Fernand Nathan, 1977, p. 42
- GEPS de matemáticas, documento adjunto 1er S, 08-01-2001, P. 7/30
- A menos que sea el ángulo plano o el ángulo cero .
- Audin , 2006 , p. 73-74.
- Audin , 2006 , p. 75.
- Audin , 2006 , p. 76.
- Daniel Perrin, Acerca de los ángulos orientados , p.4.
- Marie-Claude Davis, Frédéric Haglund y Daniel Perrin, euclidiana geometría afín , la Capes 2009-2010, Université Paris Sud Orsay, p. 27-28.
- "Ángulo de dos líneas" hoja en la geometría y la teoría de algoritmos sitio de la Universidad de Lieja
- Colectivo (dir. W. Gellert, H. Küstner, M. Hellwich, H. Kästner) ( traducido bajo la dirección de Jacques-Louis Lions, profesor del College de France), Pequeña enciclopedia de matemáticas [“Kleine Enzyklopädie der Mathematik »], París, Didier ,1997( 1 st ed. 1980), 896 p. ( ISBN 978-2-278-03526-7 ) , pág. 585.
- Se supone aquí que la Tierra es esférica, que no es del todo cierto: su forma general está ligeramente aplanado en los dos polos, y sus asperezas presenta superficiales (fosas oceánicas, montañas).
Ver también
Artículos relacionados
- Ángulo (teledetección)
- Ángulo mágico
- Angulación
- Ángulo del trihedro
- Coordenadas polares
- Geometría vectorial
- El teorema de la bisectriz
- Sistema de coordenadas ecuatoriales
enlaces externos
- (es) " Ángulos " , en Math Open Reference
- (en) David A. Wallis, “History of Angle Measurement” , en Proceedings, FIG Workshop Week 2005 y 8ª Conferencia Internacional sobre la Infraestructura Global de Datos Espaciales , El Cairo ,Abril de 2005( leer en línea )
Bibliografía
- Gilles Cohen (dir.), Les angles sous tous les angles , Bibliothèque Tangente, Número 53, Editions Pôle Paris, 2015, (Presentación online) .


























![(u, v) + (z, t): = S ^ {- 1} [S (u, v) \ circ S (z, t)]](https://wikimedia.org/api/rest_v1/media/math/render/svg/d998eb6d32dfd837881d5e03e1603ae2f9edd27c)



