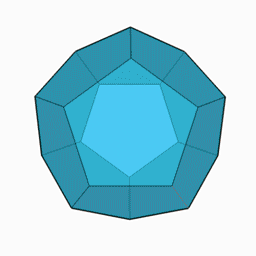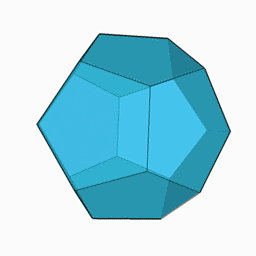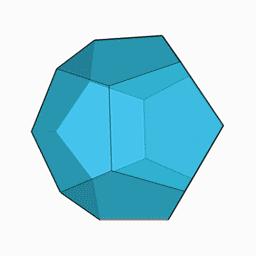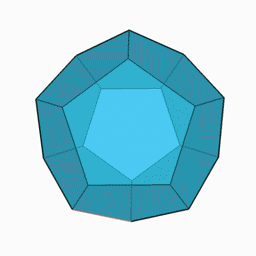
Dodecaedro regular

Dodecaedro regular


Tipo	Sólido platónico
Caras	12 pentágonos regulares
Bordes	30
Vértices	20
Caras / vértice	3
Característica	2

Símbolo de Schläfli	{5.3}
Símbolo de Wythoff	3
Diagrama de Coxeter-Dynkin
Doble	Icosaedro
Grupo de simetría	Yo h
Volumen	${\ Displaystyle {\ tfrac {15 + 7 {\ sqrt {5}}} {4}} a ^ {3}}$
Área	${\ Displaystyle 3 {\ sqrt {25 + 10 {\ sqrt {5}}}} a ^ {2}}$
Ángulo diedro	arcos (-1 / √ 5 ) ( 116,565 05 ° )
Propiedades	Convexo , regular

El dodecaedro regular es un dodecaedro cuyas 12 caras son pentágonos regulares . Tiene 30 aristas y 20 vértices . Es uno de los 5 sólidos de Platón . Tiene una esfera circunscrita que pasa por sus 20 vértices y una esfera inscrita tangente a sus 12 caras.

Dado que tiene 5 vértices por cara y 3 caras por vértice, su símbolo de Schläfli es {5.3}.

El prefijo dodeca- , doce en griego antiguo , se refiere al número de caras. Su poliedro dual es el icosaedro regular.

Cantidades características

Si $a$ es la longitud de un borde:

el radio de su esfera circunscrita es: donde está el número áureo ; ${\ Displaystyle R = {\ sqrt {3}} \; {\ frac {1 + {\ sqrt {5}}} {4}} \; a = {\ frac {\ sqrt {3}} {2}} \; \ varphi \; a}$ ${\ Displaystyle \ varphi = {\ frac {1 + {\ sqrt {5}}} {2}}}$
su área es :; ${\ Displaystyle A = 3 {\ sqrt {25 + 10 {\ sqrt {5}}}} \; a ^ {2} = 3 {\ sqrt {5 (3 + 4 \ varphi)}} \; a ^ { 2}}$
su volumen es :; ${\ Displaystyle V = {\ frac {15 + 7 {\ sqrt {5}}} {4}} \; a ^ {3} = {\ frac {4 + 7 \ varphi} {2}} \; a ^ {3}}$
su ángulo diedro (entre dos caras) es :; ${\ Displaystyle \ arccos \ left (- {\ frac {1} {\ sqrt {5}}} \ right) = \ operatorname {arccot} \ left (- {\ frac {1} {2}} \ right) \ simeq 116 {,} 565 ^ {\ circ}}$
los 20 puntos de coordenadas son los vértices de un dodecaedro regular centrado en el origen y el borde . ${\ Displaystyle \ left (0, \ pm {\ frac {1} {\ varphi}}, \ pm \ varphi \ right), \ quad \ left (\ pm {\ frac {1} {\ varphi}}, \ pm \ varphi, 0 \ right), \ quad \ left (\ pm \ varphi, 0, \ pm {\ frac {1} {\ varphi}} \ right), \ quad (\ pm 1, \ pm 1, \ pm 1)}$ ${\ Displaystyle a = {\ frac {2} {\ varphi}}}$

Simetrías

El dodecaedro admite un centro de simetría.

Las isometrías que dejan el dodecaedro regular globalmente invariante forman un grupo . Este grupo contiene:

las rotaciones del eje que pasan por 2 vértices opuestos y del ángulo 2π / 3 o 4π / 3 (120 ° y 240 °). Hay 10 pares de vértices opuestos, por lo que 20 rotaciones de este tipo;
las rotaciones del eje pasan por el centro de 2 caras opuestas y del ángulo 2π / 5, 4π / 5, 6π / 5 u 8π / 5 (72 °, 144 °, 216 ° y 288 °). Como hay 6 pares de caras opuestas, hay 24 rotaciones de este tipo;
las rotaciones de un ángulo π (180 °) alrededor de un eje que pasa por el medio de 2 bordes opuestos (estas rotaciones también son simetrías axiales). Hay 15 pares de bordes opuestos y, por lo tanto, 15 rotaciones de este tipo;
simetría s con respecto a su centro;
las simetrías con respecto a un plano que pasa por el centro y perpendicular a uno de los 15 ejes mencionados anteriormente;
etc.

Con la identidad, las 20 + 24 + 15 rotaciones indicadas forman un subgrupo de 60 elementos isomorfos al grupo alterno A 5 . De hecho, cualquier rotación permuta los cinco cubos que forman el dodecaedro y, a la inversa, cualquier permutación uniforme de los cinco cubos define una sola rotación.

Asimismo, la identidad y la simetría s forman otro subgrupo denominado C 2 .

El grupo de isometrías anotado es el producto de sus dos subgrupos; ${\ Displaystyle I_ {h}}$

contiene 120 elementos.

Propiedades misceláneas

El dodecaedro regular y el icosaedro regular son duales entre sí, es decir que el poliedro que tiene por vértices los centros de las caras de uno es el homotético del otro.

El esqueleto del dodecaedro regular, el conjunto de sus vértices conectados por sus bordes, forma un gráfico llamado gráfico dodecaedro .

Platón puso el dodecaedro en correspondencia con el Todo porque es el sólido que más se parece a la esfera. Aristóteles nombró a este quinto elemento, aithêr ( éter en latín, "éter" en francés) y postuló que el universo estaba hecho de este elemento, y que era sustancial para todos los demás, que los contenía a todos.

Demostración de la existencia de un centro de simetría.

Sea O el centro del dodecaedro (punto equidistante de sus vértices) y A un vértice. La línea OA interseca el dodecaedro en un segundo punto K, que es el centro de una cara, el punto medio de una arista o un vértice. Sin embargo, las dos rotaciones del eje OA y de los respectivos ángulos 1/3 y 2/3 de vuelta transforman el dodecaedro en sí mismo. Por tanto, K solo puede ser un vértice, y la simétrica del vértice A con respecto a O es el vértice K.

El dodecaedro admite cinco tripletes de planos ortogonales que pasan por el centro y que son cada uno de los planos de simetría del dodecaedro.

Demostración

Sea AB una arista con el centro M y KL la arista simétrica de AB con respecto al centro O.

La simetría con respecto al plano perpendicular a OM que pasa por O es el producto de la rotación de una media vuelta del eje OM por la simetría del centro O.

La simetría S del eje que pasa por O y paralelo a AB y que transforma AB en LK, forma parte de las 15 rotaciones del grupo H de media vuelta conservando el dodecaedro. La simetría con respecto al plano que pasa por O y perpendicular a AB es el producto de S por la simetría con el centro O.

La simetría T del eje que pasa por O y perpendicular al plano AOB y que transforma AB en KL, forma parte de las 15 rotaciones del grupo H de media vuelta conservando el dodecaedro. La simetría con respecto al plano que pasa por AOB es el producto de T por la simetría del centro O

Los tres planos ortogonales que pasan por O, respectivamente perpendiculares a OM, a AB ya los dos precedentes, son por tanto tres de los quince planos de simetría del dodecaedro. Mediante cuatro rotaciones de ángulos 1/5, 2/5, 3/5 y 4/5 de vuelta, de eje común con la cara que contiene A y no B, se obtienen otros cuatro tripletes de planos de simetría ortogonales.

Construcción

1. Construcción de las tres primeras caras.

Sea ABCDE un pentágono regular que constituye la primera cara F1, con centro O y borde de longitud a. En el plano ABC, la perpendicular a AB que pasa por E interseca la recta OA en H. En el plano que pasa por OAH y perpendicular al plano ABC, sea G uno de los dos puntos de intersección de la perpendicular al plano en H con el círculo con centro A y radio a. Los puntos E y G están en el mismo plano perpendicular a AB y a la misma distancia de AB. Por lo tanto, hay una rotación del eje AB que transforma E en G. Sea F3 la transformada de F1 por esta rotación: es un pentágono regular que tiene el borde común AB con F1. Sea F2 el simétrico de F3 con respecto al plano OAG: es un pentágono regular que tiene la arista común AB con F1 y la arista común AG con F3.

2. Construcción de las siguientes tres caras.

Sea R la rotación del eje que pasa por O y perpendicular al plano ABC y de 1/5 de vuelta. Transforma la cara F2 en la cara F3, porque los planos EAG y ABG forman el mismo ángulo con el plano ABC. Sean F4, F5 y F6 las transformadas de F2 por las respectivas rotaciones R 2 , R 3 y R 4 . F2 tiene un borde común con F3, por lo que F6 tiene un borde común con R 4 (F3), que es igual a R 5 (F2) o F2.

3. Construcción de las últimas seis caras.

Sea S la rotación del eje que pasa por el centro de la cara F2 y perpendicular a ella, y en 1/5 de vuelta. Transforma las caras F1 y F3 respectivamente en las caras F6 y F1, porque los planos de F1, F3 y F6 forman el mismo ángulo con el plano de F2. Además, la cara F4 tiene un borde común con F1 y un borde común con F3, pero no tiene un borde común con F2. Su transformada S (F4) tiene, por tanto, una arista común con F6 y con F1, pero ninguna con F2: por tanto, es F5.

Sean F7 y F8 las transformadas de F1 por las rotaciones respectivas S 2 y S 3 . F1 tiene un borde común con F6, F8 tiene un borde común con F3.

Sean F9, F10 y F11 las transformadas de F4 por las respectivas rotaciones S 2 , S 3 y S 4 . F4 tiene un borde común con F5, F11 tiene un borde común con F4.

El borde de F4 que no es común con ninguna de las otras diez caras definidas anteriormente, se transforma por S, S 2 , S 3 y S 4 en un borde respectivamente de F5, F9, F10 y F11, que están en un mismo plano y forman un pentágono regular, duodécima cara del dodecaedro.

Usos

El poeta medieval Jean de Meung ( 1240 - 1305 ) describió un juego de mesa adivinatorio , llamado "dodechedron", que utiliza un dado en forma de dodecaedro regular, cada una de las doce caras de las cuales representa uno de los signos del Zodíaco .

El Megaminx es un rompecabezas derivado del cubo de Rubik en forma de dodecaedro regular.

Algunos juegos de rol de mesa usan dados de 12 caras en su sistema de juego para la resolución de la acción. Estos dados de 12 caras son dodecaedros.

Notas y referencias

Jean de Meung, Le dodechedron de fortune: un libro no menos placentero y recreativo, que sutil e ingenioso entre todos los juegos y pasar el tiempo de la fortuna , Nicolas Bonfons , París, 1577 .