Ley de Poisson

Ley de Poisson

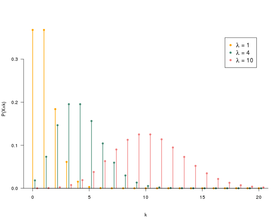Función de masa Las funciones de masa solo se definen para los números enteros $k$ .
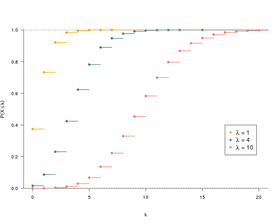Función de distribución

configuraciones	$\ lambda \ in {}] 0, + \ infty [$
Apoyo	$\ mathbb {N}$
Función de masa	${\ Displaystyle {\ frac {\ mathrm {e} ^ {- \ lambda} \ lambda ^ {k}} {k!}} \!}$
Función de distribución	${\ displaystyle {\ frac {\ Gamma (\ lfloor k + 1 \ rfloor, \ lambda)} {\ lfloor k \ rfloor!}} \! {\ text {para}} k \ geq 0}$ (donde es la función gamma incompleta ) y donde es la parte entera predeterminada de x $\ Gamma (x, y)$ $\ lfloor x \ rfloor$
Esperanza	$\ lambda \,$
Mediana	$\ text {acerca de} \ lfloor \ lambda + 1 / 3-0.02 / \ lambda \ rfloor$
Moda	$\ lfloor \ lambda \ rfloor$ si es un real no entero, $\ lambda$ $\ lambda$ y si es un entero $\ lambda-1$ $\ lambda$
Diferencia	$\ lambda \,$
Asimetría	$\ lambda ^ {- 1/2} \,$
Curtosis normalizada	$\ lambda ^ {- 1} \,$
Entropía	${\ Displaystyle \ lambda [1 \! - \! \ log (\ lambda)] \! + \! \ mathrm {e} ^ {- \ lambda} \ sum _ {k = 0} ^ {\ infty} {\ frac {\ lambda ^ {k} \ log (k!)} {k!}}.}$ Para grandes: $\ lambda$ ${\ Displaystyle \ scriptstyle {\ frac {1} {2}} \ log (2 \ pi \ mathrm {e} \ lambda) - {\ frac {1} {12 \ lambda}} - {\ frac {1} { 24 \ lambda ^ {2}}} - {\ frac {19} {360 \ lambda ^ {3}}} + O \ left ({\ frac {1} {\ lambda ^ {4}}} \ right)}$
Función generadora de momentos	${\ Displaystyle \ exp (\ lambda (e ^ {t} -1))}$
Función característica	${\ Displaystyle \ exp (\ lambda (\ mathrm {e} ^ {it} -1)) \,}$
Función generadora de probabilidad	${\ Displaystyle \ exp (\ lambda (t-1))}$

En teoría de probabilidad y estadística , la ley de Poisson es una ley de probabilidad discreta que describe el comportamiento del número de eventos que ocurren en un intervalo de tiempo fijo, si estos eventos ocurren con una frecuencia o expectativa promedio conocida, e independientemente del tiempo transcurrido desde el anterior. evento.

La ley de Poisson también es relevante para describir el número de eventos en otros tipos de intervalos, espaciales más que temporales, como segmentos, áreas o volúmenes.

Historia

La ley de Poisson fue introducida en 1838 por Denis Poisson (1781-1840), en su obra Recherches sur la probabilidad de juicios en asuntos penales y civiles . El tema principal de este libro consiste en ciertas variables aleatorias que cuentan, entre otras cosas, el número de ocurrencias (a veces llamadas "llegadas") que tienen lugar durante un período de tiempo determinado.

Definición

Si el número promedio de ocurrencias en un intervalo de tiempo fijo es $λ$ , entonces la probabilidad de que haya exactamente $k$ ocurrencias ( siendo $k$ un entero natural , $k = 0, 1, 2\dots$ ) es ${\ Displaystyle p (k) = \ mathbb {P} (X = k) = {\ frac {\ lambda ^ {k}} {k!}} \ mathrm {e} ^ {- \ lambda}}$ o :

$e$ es la base de la exponencial ( $e \approx 2.718 ...$ );
$k !$ es el factorial de $k$ ;
$λ$ es un número real estrictamente positivo .

Luego decimos que $X$ sigue la ley de Poisson del parámetro $λ$ , denotado . ${\ Displaystyle X \ sim \ operatorname {Pois} \ left (\ lambda \ right)}$

Por ejemplo, si un determinado tipo de evento ocurre en promedio 4 veces por minuto , para estudiar el número de eventos que ocurren en un período de 10 minutos, elegimos como modelo una distribución de Poisson con parámetro $λ = 10 \times 4 = 40$ .

Cálculo de p ( k )

Este cálculo se puede hacer deductivamente trabajando en una distribución binomial de parámetros ( $T$ ; $λ / T$ ). Para $T$ grande, probamos que la ley binomial converge con la ley de Poisson.

También se puede realizar de forma inductiva estudiando el intervalo $[0; T ]$ las funciones $F k ( t )$ , que dan la probabilidad de que el evento ocurra $k$ veces durante el intervalo de tiempo $[0; t ]$ . Mediante el uso de recurrencia y cálculo diferencial, logramos encontrar las fórmulas anteriores.

Propiedades

A lo largo de esta sección, $X$ es una variable aleatoria que sigue una ley de Poisson con el parámetro $λ$ .

Momentos y funciones generadoras

Momentos ordinarios

Los primeros cuatro momentos ordinarios de una distribución de Poisson están dados por:

${\ Displaystyle {\ begin {array} {lll} \ mathbb {E} [X] & = & \ lambda \\\ mathbb {E} [X ^ {2}] & = & \ lambda (1+ \ lambda) \\\ mathbb {E} [X ^ {3}] & = & \ lambda (1 + 3 \ lambda + \ lambda ^ {2}) \\\ mathbb {E} [X ^ {4}] & = & \ lambda (1 + 7 \ lambda +6 \ lambda ^ {2} + \ lambda ^ {3}) \ end {matriz}}}$

Deducimos la varianza y la desviación estándar :

${\ Displaystyle {\ begin {array} {lll} V (X) & = & \ lambda \\\ sigma (X) & = & {\ sqrt {\ lambda}} \ end {array}}}$

Más generalmente, el $n$ º tiempo ordinario un parámetro de Poisson $λ$ es decir ${\ Displaystyle \ mathbb {E} (X ^ {n}) = \ sum _ {k = 0} ^ {n} S (n, k) \ lambda ^ {k}}$ donde $S ( n , k )$ es el número de Stirling del segundo tipo de parámetros y . $no$ $k$

En particular cuando el $n-$ ésimo momento de $X$ corresponde al $n-$ ésimo número de Bell . De hecho, esto es una consecuencia de la fórmula de Dobiński . $\ lambda = 1$

El siguiente límite magnifica los momentos de una distribución de Poisson: ${\ Displaystyle \ mathbb {E} [X ^ {n}] \ leq {\ frac {k ^ {k}} {\ ln \ left ({\ frac {k} {\ lambda}} + 1 \ right)} } \ leq \ lambda ^ {k} e ^ {\ frac {k} {2 \ lambda}}}$ Tenemos la relación de recurrencia: ${\ Displaystyle \ mathbb {E} [X ^ {n}] = \ lambda \ mathbb {E} [X ^ {n-1}] + \ lambda {\ frac {\ partial \ mathbb {E} [X ^ { n-1}]} {\ parcial \ lambda}}}$

Momentos centrados

Los primeros cuatro momentos centrados de una distribución de Poisson están dados por:

${\ Displaystyle {\ begin {array} {lll} \ mathbb {E} [(X- \ lambda) ^ {2}] & = & \ lambda \\\ mathbb {E} [(X- \ lambda) ^ { 3}] & = & \ lambda \\\ mathbb {E} [(X- \ lambda) ^ {4}] & = & \ lambda (1 + 3 \ lambda) \\\ mathbb {E} [(X- \ lambda) ^ {5}] & = & \ lambda (1 + 10 \ lambda) \ end {matriz}}}$

Deducimos la asimetría y la curtosis normalizada :

${\ Displaystyle {\ begin {array} {lll} \ gamma _ {1} (X) & = & 1 / {\ sqrt {\ lambda}} \\\ gamma _ {2} (X) & = & 1 / \ lambda \ end {matriz}}}$

Tenemos la relación de recurrencia: ${\ Displaystyle \ mathbb {E} [(X- \ lambda) ^ {n + 1}] = n \ lambda \ mathbb {E} [(X- \ lambda) ^ {n-1}] + \ lambda {\ frac {\ parcial \ mathbb {E} [(X- \ lambda) ^ {n}]} {\ parcial \ lambda}}}$

Momentos factoriales

El $r-$ ésimo momento factorial de una distribución de Poisson es

${\ Displaystyle \ mathbb {E} ((X) _ {r}) = \ lambda ^ {r}}$

donde denota el factorial decreciente . ${\ Displaystyle (x) _ {r} = x (x-1) \ dots (x-r + 1)}$

Función generadora de probabilidad

La función que genera las probabilidades de una distribución de Poisson es

${\ Displaystyle G_ {X} (t) \ equiv \ mathbb {E} (t ^ {X}) = \ mathrm {e} ^ {\ lambda (t-1)}.}$

Función generadora de momentos

La función generadora de los momentos de una distribución de Poisson es

${\ Displaystyle M_ {X} (t) \ equiv \ mathbb {E} (\ mathrm {e} ^ {tX}) = \ exp \ left (\ lambda (\ mathrm {e} ^ {t} -1) \ derecho).}$

Demostración

Sea $X$ una variable aleatoria que sigue una distribución de Poisson con el parámetro $λ$ . Recuerda eso por definición . ${\ Displaystyle \ mathbb {P} (X = k) = \ mathrm {e} ^ {- \ lambda} {\ frac {\ lambda ^ {k}} {k!}}}$

Esperanza

{\ Displaystyle {\ begin {alineado} \ mathbb {E} (X) & = \ sum _ {k = 1} ^ {\ infty} k \, \ mathbb {P} (X = k) \\ & = \ suma _ {k = 1} ^ {\ infty} k \, \ mathrm {e} ^ {- \ lambda} {\ frac {\ lambda ^ {k}} {k!}} \\ & = \ mathrm {e } ^ {- \ lambda} \, \ sum _ {k = 1} ^ {\ infty} {\ frac {\ lambda ^ {k}} {(k-1)!}} \\ & = \ lambda \, \ mathrm {e} ^ {- \ lambda} \, \ sum _ {k = 1} ^ {\ infty} {\ frac {\ lambda ^ {k-1}} {(k-1)!}} \ qquad ({\ text {reconocemos la expansión serial entera de}} \ mathrm {e} ^ {\ lambda}) \\ & = \ lambda \, \ mathrm {e} ^ {- \ lambda} \, \ mathrm {e } ^ {\ lambda} \\ & = \ lambda. \ end {alineado}}}

Diferencia

{\ Displaystyle {\ begin {alineado} V (X) & = \ mathbb {E} (X ^ {2}) - (\ mathbb {E} (X)) ^ {2} & \\ & = \ sum _ {k = 1} ^ {\ infty} k ^ {2} \, \ mathbb {P} (X = k) - \ lambda ^ {2} & \\ & = \ sum _ {k = 1} ^ {\ infty} k ^ {2} \, \ mathrm {e} ^ {- \ lambda} {\ frac {\ lambda ^ {k}} {k!}} - \ lambda ^ {2} & \\ & = \ lambda \, \ mathrm {e} ^ {- \ lambda} \ sum _ {k = 1} ^ {\ infty} \, {\ frac {k \ lambda ^ {k-1}} {(k-1)!} } - \ lambda ^ {2} & \\ & = \ lambda \, \ mathrm {e} ^ {- \ lambda} \ sum _ {k = 1} ^ {\ infty} \, {\ frac {d} { d \ lambda}} {\ frac {\ lambda ^ {k}} {(k-1)!}} - \ lambda ^ {2} & \ qquad ({\ text {toda la serie que tiene un radio de convergencia infinito,} } \\ & = \ lambda \, \ mathrm {e} ^ {- \ lambda} {\ frac {d} {d \ lambda}} \ sum _ {k = 1} ^ {\ infty} \, {\ frac {\ lambda ^ {k}} {(k-1)!}} - \ lambda ^ {2} & \ qquad {\ text {podemos invertir la suma y la derivación}}) \\ & = \ lambda \, \ mathrm {e} ^ {- \ lambda} {\ frac {d} {d \ lambda}} \ left [\ lambda \ sum _ {k = 1} ^ {\ infty} \, {\ frac {\ lambda ^ {k-1}} {(k-1)!}} \ right] - \ lambda ^ {2} & \ qquad ({\ text {reconocemos la expansión serial entera de}} \ mathrm {e} ^ {\ lambda}) \\ & = \ lambda \, \ mathrm {e} ^ {- \ lambda} {\ frac {d} {d \ lambda}} [\ lambda \, \ mathrm {e} ^ {\ lambda}] - \ lambda ^ {2} & \\ & = \ lambda \, \ mathrm {e} ^ {- \ lambda} (\ lambda +1) \, \ mathrm {e} ^ {\ lambda} - \ lambda ^ {2} & \\ & = \ lambda \, (\ lambda +1 ) - \ lambda ^ {2} & \\ & = \ lambda. & \ end {alineado}}}

Función de generador

Recordamos que la función generadora de $X$ está definida por . Entonces obtenemos: ${\ Displaystyle G_ {X} (t) = \ mathbb {E} (t ^ {X})}$

{\ Displaystyle {\ begin {alineado} \ mathbb {E} (t ^ {X}) & = \ sum _ {k = 0} ^ {\ infty} t ^ {k} \ mathbb {P} (X = k ) \\ & = \ sum _ {k = 0} ^ {\ infty} t ^ {k} \ mathrm {e} ^ {- \ lambda} {\ frac {\ lambda ^ {k}} {k!}} \\ & = \ mathrm {e} ^ {- \ lambda} \ sum _ {k = 0} ^ {\ infty} t ^ {k} {\ frac {\ lambda ^ {k}} {k!}} \ \ & = \ mathrm {e} ^ {- \ lambda} \ sum _ {k = 0} ^ {\ infty} {\ frac {(t \ lambda) ^ {k}} {k!}} \ qquad ({ \ text {reconocemos la expansión serial entera de}} \ mathrm {e} ^ {t \ lambda}) \\ & = \ mathrm {e} ^ {- \ lambda} \ mathrm {e} ^ {t \ lambda} \\ & = \ mathrm {e} ^ {\ lambda (t-1)}. \ end {alineado}}}

Función generadora de momentos

Recordemos que la función generadora de los momentos de $X$ está definida por . Entonces obtenemos: ${\ Displaystyle M_ {X} (t) = \ mathbb {E} (\ mathrm {e} ^ {tX})}$

{\ Displaystyle {\ begin {alineado} M_ {X} (t) & = \ sum _ {k = 0} ^ {\ infty} \ mathrm {e} ^ {tk} \ mathbb {P} (X = k) \\ & = \ sum _ {k = 0} ^ {\ infty} \ mathrm {e} ^ {tk} {\ frac {\ lambda ^ {k}} {k!}} \, \ mathrm {e} ^ {- \ lambda} \\ & = \ mathrm {e} ^ {- \ lambda} \ sum _ {k = 0} ^ {\ infty} {\ frac {(\ lambda \, \ mathrm {e} ^ {t }) ^ {k}} {k!}} \ qquad ({\ text {reconocemos la expansión de la serie entera de}} \ mathrm {e} ^ {x} {\ text {evaluado en}} x = \ lambda \ mathrm {e} ^ {t}) \\ & = \ mathrm {e} ^ {- \ lambda} \ mathrm {e} ^ {\ lambda \, \ mathrm {e} ^ {t}} \\ & = \ mathrm {e} ^ {\ lambda (\ mathrm {e} ^ {t} -1)}. \ end {alineado}}}

Momentos factoriales

{\ Displaystyle {\ begin {alineado} \ mathbb {E} ((X) _ {r}) & = \ mathrm {e} ^ {- \ lambda} \ sum _ {k = r} ^ {\ infty} { \ frac {k!} {(kr)!}} {\ frac {\ lambda ^ {k}} {k!}} \\ & = \ lambda ^ {r} \ mathrm {e} ^ {- \ lambda} \ sum _ {k = r} ^ {\ infty} {\ frac {\ lambda ^ {kr}} {(kr)!}} \\ & = \ lambda ^ {r} \ mathrm {e} ^ {- \ lambda} \ sum _ {k = 0} ^ {\ infty} {\ frac {\ lambda ^ {k}} {k!}} \\ & = \ lambda ^ {r}. \ end {alineado}}}

Momentos

Los números de Stirling del segundo tipo verifican la relación

{\ Displaystyle X ^ {n} = \ sum _ {k = 0} ^ {n} S (n, k) (X) _ {k}}

Por lo tanto, al usar la fórmula de los momentos factoriales de una ley de Poisson, así como la linealidad de la expectativa, concluimos que

{\ Displaystyle \ mathbb {E} (X ^ {n}) = \ sum _ {k = 0} ^ {n} S (n, k) \ lambda ^ {k}}

Gráfico de barras

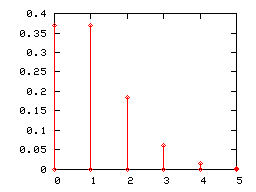
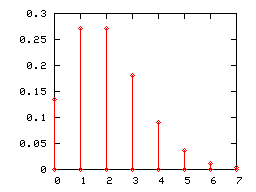
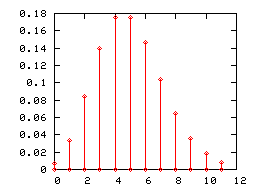
Como cualquier ley de probabilidad discreta , una ley de Poisson se puede representar mediante un gráfico de barras. A continuación se muestran los diagramas de barras de las leyes de Poisson de los parámetros 1, 2 y 5.

Cuando el parámetro de la ley de Poisson $λ se$ vuelve grande (prácticamente cuando es mayor que 5), su diagrama de barras se aproxima correctamente mediante el histograma de una ley normal de expectativa y varianza igual a $λ$ (l 'intervalo de clase es igual a la unidad). Esta convergencia se aprovechó, antes de que se generalizaran los recursos informáticos, para utilizar la ley normal en lugar de la ley de Poisson en determinadas pruebas.

Estabilidad de la distribución de Poisson por la suma

Si las variables ${ X i } i = 1, ..., n$ son independientes y siguen una ley de Poisson con parámetros respectivos $λ i$ , entonces su suma sigue una ley de Poisson con parámetro la suma de $λ i$ : ${\ Displaystyle Y = \ left (\ sum _ {i = 1} ^ {n} X_ {i} \ right) \ sim \ operatorname {Pois} \ left (\ sum _ {i = 1} ^ {n} \ lambda _ {i} \ right)}$

Demostración

Mostramos el caso $n = 2$ , los casos superiores se deducen por inducción.

Recuérdalo ${\ Displaystyle \ mathbb {P} (X_ {1} = n) = {\ frac {{\ lambda _ {1}} ^ {n}} {n!}} \ mathrm {e} ^ {- \ lambda _ {1}} {\ text {y}} \ mathbb {P} (X_ {2} = n) = {\ frac {{\ lambda _ {2}} ^ {n}} {n!}} \ Mathrm { e} ^ {- {\ lambda _ {2}}}.}$ Entonces tenemos ${\ Displaystyle {\ begin {alineado} \ mathbb {P} (X + Y = n) & = \ sum _ {k = 0} ^ {n} \ mathbb {P} (\ {X_ {1} = k \ } \ cap \ {X_ {2} = nk \}) = \ sum _ {k = 0} ^ {n} \ mathbb {P} (X_ {1} = k) \ mathbb {P} (X_ {2} = nk) \\ & = \ sum _ {k = 0} ^ {n} {\ frac {\ lambda _ {1} ^ {k}} {k!}} \ mathrm {e} ^ {- \ lambda _ {1}} \ cdot {\ frac {\ lambda _ {2} ^ {nk}} {(nk)!}} \ Mathrm {e} ^ {- \ lambda _ {2}} \\ & = {\ frac {\ mathrm {e} ^ {- \ lambda _ {1}} \ mathrm {e} ^ {- \ lambda _ {2}}} {n!}} \ sum _ {k = 0} ^ {n} { \ frac {n!} {k! (nk)!}} \ lambda _ {1} ^ {k} \ lambda _ {2} ^ {nk} = {\ frac {\ mathrm {e} ^ {- (\ lambda _ {1} + \ lambda _ {2})}} {n!}} (\ lambda _ {1} + \ lambda _ {2}) ^ {n} \ end {alineado}}}$

La independencia se utilizó en 2 e iguales. La última igualdad se obtiene mediante la fórmula binomial de Newton .

Terminales de cola

Un argumento de tipo Chernoff bound permite deducir los siguientes límites de cola

{\ Displaystyle \ mathbb {P} (X \ geq x) \ leq {\ frac {\ mathrm {e} ^ {- \ lambda} (\ mathrm {e} \ lambda) ^ {x}} {x ^ {x }}}}

para todo

x > λ

{\ Displaystyle \ mathbb {P} (X \ leq x) \ leq {\ frac {\ mathrm {e} ^ {- \ lambda} (\ mathrm {e} \ lambda) ^ {x}} {x ^ {x }}}}

para todo

x <λ

Estos terminales se pueden reescribir de la siguiente manera

{\ Displaystyle \ mathbb {P} (X \ geq x + \ lambda) \ leq \ mathrm {e} ^ {- {\ frac {x ^ {2}} {2 \ lambda}} h \ left ({\ frac {x} {\ lambda}} \ right)}}

para todo

x > 0

{\ Displaystyle \ mathbb {P} (X \ leq -x + \ lambda) \ leq \ mathrm {e} ^ {- {\ frac {x ^ {2}} {2 \ lambda}} h \ left (- { \ frac {x} {\ lambda}} \ right)}}

para todo

λ> x > 0

donde para todo . Estos últimos límites implican en particular el siguiente bolardo (que es más débil pero más agradable de manejar) ${\ Displaystyle h (u): = 2 {\ frac {(1 + u) \ ln (1 + u) -u} {u ^ {2}}}}$ ${\ Displaystyle u \ geq -1}$

{\ Displaystyle \ mathbb {P} (| X- \ lambda | \ geq x) \ leq 2 \ mathrm {e} ^ {- {\ frac {x ^ {2}} {2 (\ lambda + x)}} }}

El límite superior dado por Chernoff se puede mejorar en un factor de al menos 2

{\ Displaystyle \ mathbb {P} (X \ geq x + \ lambda) \ leq {\ frac {\ mathrm {e} ^ {- {\ frac {x ^ {2}} {2 \ lambda}} h \ left ({\ frac {x} {\ lambda}} \ right)}} {\ max \ left \ {2, {\ sqrt {{\ frac {2 \ pi x ^ {2}} {\ lambda}} h \ izquierda ({\ frac {x} {\ lambda}} \ right)}} \ right \}}}}

para todo

x > 0

Cabe señalar que la función $h$ está vinculada a la divergencia de Kullback-Leibler entre una ley de Poisson con parámetro $x + λ$ y una ley de Poisson con parámetro $λ$ . De hecho tenemos la relación

{\ Displaystyle D_ {KL} (x + \ lambda || \ lambda) = (x + \ lambda) \ ln \ left ({\ frac {x} {\ lambda}} + 1 \ right) -x = {\ frac {x ^ {2}} {2 \ lambda}} h \ left ({\ frac {x} {\ lambda}} \ right)}

Simulación

Un algoritmo simple para simular la ley de Poisson es usar el siguiente resultado:

Teorema - Sea $( E i ) i \geq 1$ una secuencia de variables aleatorias independientes con la misma distribución exponencial con el parámetro $λ$ . Establecemos $S 1 = E 1$ y para $n \geq 2$ , $S n = E 1 + ... + E n$ . Entonces tenemos:

{\ Displaystyle \ forall n \ geqslant 1, \ \ mathbb {P} (S_ {n} \ leqslant 1 <S_ {n + 1}) = {\ frac {\ mathrm {e} ^ {- \ lambda} \ lambda ^ {n}} {n!}}.}

El método de transformación inversa proporciona una forma sencilla de generar un sorteo aleatorio de acuerdo con una ley exponencial:

U

sigue una ley uniforme en

[0; 1]

, entonces

E = - 1 / λ ln ( U )

sigue una ley exponencial con parámetro

λ

Por tanto, el algoritmo se puede simplificar mediante:

$k \leftarrow 0$ , $p \leftarrow 1$
siempre que p > e –λ
- dibujamos $u de$ acuerdo con un sorteo aleatorio uniforme en $[0; 1]$
- $p \leftarrow p \times u$
- $k \leftarrow k +1$
devolvemos $k - 1$

Estimación del parámetro $λ$

El estimador de máxima verosimilitud del parámetro $λ$ de una muestra derivada de una distribución de Poisson es la media empírica . Es un estimador de convergencia sin sesgos , eficaz , integral (in) , exhaustivo .

Vínculo con otras leyes de probabilidad

Si $X$ e $Y$ son dos variables aleatorias independientes que siguen las leyes de Poisson de los parámetros respectivos $λ$ y $μ$ , entonces $X - Y$ es una variable aleatoria que sigue una ley de parámetros de Skellam $(λ, μ )$ .
Si $X$ e $Y$ son dos variables aleatorias independientes que siguen las leyes de Poisson con parámetros $λ$ y $μ$ , entonces la ley condicional de $X$ conociendo $X + Y$ es una ley binomial .
Para valores grandes de $λ$ , podemos aproximarnos a la ley de Poisson mediante la ley normal de la media $λ$ y la varianza $λ$ .

Vínculo con la ley de Bernoulli

El recuento de eventos raros a menudo se realiza a través de una suma de variables de Bernoulli , la rareza de los eventos resulta en el hecho de que los parámetros de estas variables de Bernoulli son pequeños (por lo tanto, la probabilidad de que ocurra cada evento es baja). El vínculo entre la ley de Poisson y los eventos raros se puede establecer de la siguiente manera:

Paradigma de Poisson : la suma $S n$ de un gran número de variables independientes de Bernoulli de pequeño parámetro sigue aproximadamente la distribución de Poisson del parámetro ${\ Displaystyle \ mathbb {E} [S_ {n}]. \}$

La desigualdad de Le Cam dice que el paradigma de Poisson es una tabla de variables aleatorias independientes de Bernoulli , con los respectivos parámetros $p$ $k$ $,$ $n$ . Apuntamos ${\ Displaystyle X_ {1, n}, X_ {2, n}, \ dots, X_ {a_ {n}, n} \}$

$S_n = \ sum_ {k = 1} ^ {a_n} \, X_ {k, n} \ quad \ text {y} \ quad \ lambda_n \ = \ \ mathbb {E} [S_n] = \ sum_ {k = 1 } ^ {a_n} \, p_ {k, n}. \$

Desigualdad de Le Cam : para cualquier conjunto

A

de números naturales,

{\ Displaystyle \ left | \ mathbb {P} \ left (S_ {n} \ in A \ right) - \ sum _ {k \ in A} \, {\ frac {\ lambda _ {n} ^ {k} \, \ mathrm {e} ^ {- \ lambda _ {n}}} {k!}} \ right | \ \ leq \ \ sum _ {k = 1} ^ {a_ {n}} \, p_ {k , n} ^ {2}.}

En particular, si se cumplen las dos condiciones siguientes:

$\ lim_n \ lambda_n \, = \, \ lambda> 0, \$
$\ lim_n \ sum_ {k = 1} ^ {a_n} \, p_ {k, n} ^ 2 \, = \, 0, \$

entonces $S n$ converge de derecho a la distribución de Poisson con el parámetro Eficiencia (estadísticas)

En el enunciado del paradigma de Poisson , hacemos dos suposiciones (ondas) sobre los términos de una suma $S n$ de variables de Bernoulli:

los parámetros de las variables de Bernoulli son pequeños; sin embargo, las dos condiciones anteriores significan que

$\ lim_n \, \ left (\ max_ {1 \ le k \ le a_n} \, p_ {k, n} \ right) \, = \, 0, \$ que reformula la hipótesis “ los parámetros de las variables de Bernoulli son pequeños ” con mayor precisión;

hay una gran cantidad de términos; sin embargo, las dos condiciones anteriores conducen a que el número de términos tiende al infinito:

$\ lim_n a_n \, = \, + \ infty. \$

Notas:

Este paradigma sigue siendo relevante, bajo ciertas condiciones, si relajamos la hipótesis de la independencia .
- Un ejemplo sorprendente es el número de puntos fijos de una permutación dibujados al azar .
- Otro ejemplo es el número de puntos aislados del gráfico aleatorio , cuya convergencia hacia la ley de Poisson permitió a Erdös y Rényi demostrar, en 1960, el teorema de la doble exponencial .
El caso particular $a n = n , p k, n = λ / n , λ n = λ$ , de la desigualdad de Le Cam, especifica la velocidad de convergencia de la ley binomial de los parámetros $n$ y $λ / n$ hacia la ley de Poisson con el parámetro $λ$ .

Áreas de aplicación

El campo de aplicación de la ley de Poisson estuvo durante mucho tiempo limitado al de eventos raros como suicidios de niños, llegadas de barcos a un puerto o accidentes por patadas de caballos en ejércitos (estudio de Ladislaus Bortkiewicz ).

Pero en las últimas décadas su campo de aplicación se ha ampliado considerablemente. Actualmente, es ampliamente utilizado en telecomunicaciones (para contar el número de comunicaciones en un intervalo de tiempo determinado), control estadístico de calidad (número de defectos en SPC ), la descripción de ciertos fenómenos relacionados con la desintegración radiactiva (la desintegración de los núcleos radiactivos siguientes, además, una ley exponencial del parámetro también señaló lambda), biología ( mutaciones en el experimento de Luria y Delbrück , número de potenciales de acción emitidos por una neurona en neurociencias), meteorología , finanzas para modelar la probabilidad de incumplimiento crediticio, Yield Management ( American Airlines, Lufthansa y SAS para estimar la demanda de pasajeros), etc.

En literatura

En la novela de Thomas Pynchon , El arco iris de gravedad , uno de los personajes, el estadístico Roger México, usa la ley de Poisson para mapear las áreas de impacto de los cohetes V2 alemanes en la ciudad de Londres durante la Segunda Guerra Mundial .

Notas y referencias

Con las convenciones habituales $0! = 1$ y $0 0 = 1$ , la definición de la ley de Poisson se extiende a $λ = 0$ : entonces encontramos $p (0) = 1$ y, tan pronto como $k > 0$ , $p ( k ) = 0$ . Por lo tanto, es casi seguro que una variable aleatoria cero se puede considerar siguiendo la ley de Poisson del parámetro 0. Esta convención es consistente con las propiedades esenciales de la ley de Poisson del parámetro estrictamente positivo. Es conveniente, incluso esencial, por ejemplo, durante el estudio de los procesos puntuales de Poisson.
Siméon-Denis Poisson, Investigación sobre la probabilidad de sentencias en materia penal y civil; precedido por las Reglas generales para el cálculo de probabilidades en Gallica , 1837, pasaje 81, p. 205.
Véase, por ejemplo, Michel Henry, Alrededor del modelo de probabilidad , Presses Universitaires de Franche-Comté,2001( presentación en línea ) , pág. 229-231o estas notas del curso .
(en) Eric W. Weisstein, " distribución de Poisson " en mathworld.wolfram.com
(in) D Thomas Ahle, " Límites agudos y simples para los momentos crudos de las distribuciones Binomial y Poisson " , arXiv ,2021( arXiv 2103.17027 , leer en línea )
(en) Norman L Johnson, Adrienne W Kemp y Samuel Kotz, univariante Discrete Distribuciones , Wiley,2005, 3 e ed. ( ISBN 978-0-471-27246-5 , leer en línea ) , pág. 162
(en) Michael Mitzenmacher y Eli Upfal , Probabilidad y computación: algoritmos aleatorios y análisis probabilístico , Cambridge, Reino Unido, Cambridge University Press,2005( ISBN 978-0-521-83540-4 , leer en línea ) , pág. 97
(en) " Una breve nota sobre los límites de la cola de Poisson "
(in) Michael Short, " Desigualdades mejoradas para la distribución binomial y de Poisson y la cola superior de las funciones cuantiles " , Avisos de investigación académica internacional , vol. 2013,2013( DOI https://doi.org/10.1155/2013/412958 , leer en línea )
(in) L. Le Cam , " Un teorema de aproximación para la distribución binomial de Poisson " , Pacific Journal of Mathematics , vol. 10, n o 4,1960, p. 1181-1197 ( leído en línea , consultado el 13 de mayo de 2009 ).
(en) AD Barbour , L. Holst y S. Janson , aproximación de Poisson , Oxford, Clarendon Press, Oxford University Press,1992, 277 p. ( ISBN 0-19-852235-5 ).
Ladislaus Bortkiewicz, Das Gesetz der kleinen Zahlen ,1898( leer en línea ), p. 23 .

Ley de Poisson

Historia

Definición

Cálculo de p ( k )