Quadric

En matemáticas , una cuádrica o superficie cuadrática , es una superficie que satisface una polinomio ecuación cartesiana de grado 2 con tres variables (generalmente indicadas $x$ , $Y$ y $Z$ ) de la forma

Ax ^ 2 + Por ^ 2 + Cz ^ 2 + 2Dyz + 2Exz + 2Fxy + Gx + Hy + Iz + J = 0

Estas superficies se clasifican por una ecuación reducida en un sistema ortonormal de coordenadas adaptada en la geometría euclidiana , y en nueve no degenerados clases arriba a transformación lineal en la geometría afín . También se pueden estudiar en el marco de la geometría proyectiva , que simplifica y unifica por completo los resultados.

Sus secciones planas son cónicas .

La definición se generaliza en dimensión superior con la noción de cuadrático afín , una hipersuperficie , caracterizada como el lugar de cancelación (in) de un polinomio de grado 2, incluso en otro cuerpo de coeficientes que el de los números reales .

Clasificación

Presentación de las principales cuadrículas

Los cuádricos no degenerados se describen a continuación a partir de sus ecuaciones reducidas en un marco ortonormal adecuado.

El elipsoide	$\ frac {x ^ 2} {a ^ 2} + \ frac {y ^ 2} {b ^ 2} + \ frac {z ^ 2} {c ^ 2} -1 = 0 \,$ ,
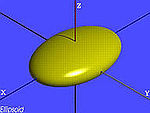
El hiperboloide de una hoja (H1)	$\ frac {x ^ 2} {a ^ 2} + \ frac {y ^ 2} {b ^ 2} - \ frac {z ^ 2} {c ^ 2} -1 = 0 \,$ ,
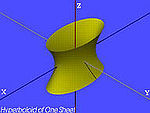
El hiperboloide de dos hojas (H2)	$\ frac {x ^ 2} {a ^ 2} + \ frac {y ^ 2} {b ^ 2} - \ frac {z ^ 2} {c ^ 2} +1 = 0 \,$ ,
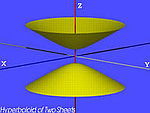
El paraboloide elíptico (PE)	$\ frac {x ^ 2} {a ^ 2} + \ frac {y ^ 2} {b ^ 2} = z \,$ ,
El paraboloide hiperbólico (PH)	$\ frac {x ^ 2} {a ^ 2} - \ frac {y ^ 2} {b ^ 2} = z \,$ ,
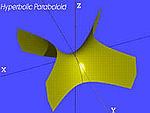
El cono base elíptico	$\ frac {x ^ 2} {a ^ 2} + \ frac {y ^ 2} {b ^ 2} - \ frac {z ^ 2} {c ^ 2} = 0 \,$ ,
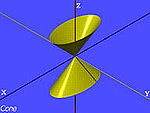
El cilindro elíptico	$\ frac {x ^ 2} {a ^ 2} + \ frac {y ^ 2} {b ^ 2} -1 = 0 \,$ ,
El cilindro hiperbólico	$\ frac {x ^ 2} {a ^ 2} - \ frac {y ^ 2} {b ^ 2} -1 = 0 \,$ ,
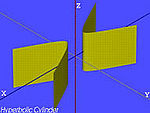
El cilindro parabólico	$\ displaystyle {x ^ 2 = 2 py}$ .

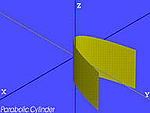
Clasificación general

La ecuación de superficie se puede escribir:

Q (x, y, z) + Gx + Hy + Iz + J = 0 ~

donde Q denota la forma cuadrática

Q (x, y, z) = Ax ^ 2 + By ^ 2 + Cz ^ 2 + 2Dyz + 2Exz + 2Fxy ~

matriz:

M_Q = \ begin {pmatrix} A & F & E \\ F & B & D \\ E & D & C \ end {pmatrix}

cuyos valores propios son todos reales ya que esta matriz es simétrica real .

La firma de la forma cuadrática es el par (p, q) donde p es el número de valores propios estrictamente positivos de Q y q el número de valores propios estrictamente negativos. El rango de Q es entonces p + q . Por definición de un cuadrático, el rango de Q no puede ser cero. El hecho de que la firma de una forma cuadrática no depende de la elección de la base elegida lo demuestra la ley de inercia de Sylvester .

Cuando el rango es igual a 3, el cuadrático admite un centro de simetría.

Rango	Firma	Cuadrico no degenerado	Cuadrico degenerado
3	(3,0) o (0,3)	elipsoide	$\ varnothing$ o apuntar
3	(2,1) o (1,2)	hiperboloide con 1 o 2 capas o cono
2	(2,0) o (0,2)	cilindro elíptico paraboloide o elíptico	$\ varnothing$ o recto
2	(1,1)	paraboloide hiperbólico o cilindro hiperbólico	reunión de dos planes
1	(1,0) o (0,1)	cilindro parabólico	$\ varnothing$ o plan o combinación de dos planes

Demostración

Para simplificar, las coordenadas siempre se anotarán x , y y z , después de los diversos cambios de marcas de referencia ortonormales que seguirán.

La matriz de la forma cuadrática, valores nominales limpias , , , se diagonalizarse utilizando una matriz de transformación ortogonal. En un nuevo sistema de coordenadas ortonormal, la ecuación de la superficie se escribe $\ alpha ~$ $\ beta ~$ $\ gamma ~$

\ alpha x ^ 2 + \ beta y ^ 2 + \ gamma z ^ 2 + px + qy + rz = k ~

Cuando uno de los valores propios es distinto de cero, por ejemplo , es posible centrar la coordenada correspondiente: $\ alpha ~$

\ alpha x ^ 2 + px = \ alpha ((x + \ frac {p} {2 \ alpha}) ^ 2 - (\ frac {p} {2 \ alpha}) ^ 2)

lo que equivale a realizar una traducción o un cambio de origen del marco de referencia.

Cuando el rango es igual a tres, los tres valores propios no son cero; en un nuevo sistema de coordenadas ortonormal, la ecuación se convierte en:

\ alpha x ^ 2 + \ beta y ^ 2 + \ gamma z ^ 2 = K ~

- si la firma vale (3.0) o (0.3), los tres valores propios tienen el mismo signo. Si K es cero, es un punto; de lo contrario, es un elipsoide si K tiene el signo de los valores propios y, en caso contrario, del conjunto vacío.
- si la firma vale (2,1) o (1,2), dos valores propios tienen el mismo signo, que se dirá aquí mayoría; si K es cero, es un cono; de lo contrario, es un hiperboloide de una hoja si K tiene el signo mayoritario y un hiperboloide de dos hojas en caso contrario.

Cuando el rango es igual a dos, uno de los valores propios es cero, y solo uno, por ejemplo ; en un nuevo sistema de coordenadas ortonormal, la ecuación se convierte en: $\ gamma ~$

\ alpha x ^ 2 + \ beta y ^ 2 + rz = K ~

- si r es distinto de cero, obtenemos un paraboloide elíptico si los dos valores propios distintos de cero tienen el mismo signo, y un paraboloide hiperbólico en caso contrario, porque la ecuación está escrita:

\ alpha x ^ 2 + \ beta y ^ 2 = - r (z - \ frac {K} {r}

- si r es cero, y si K es cero, es la unión de dos planos si los valores propios distintos de cero son de signo opuesto, y de una línea recta en caso contrario;
- si r es cero y K no es cero, es un cilindro hiperbólico si los valores propios distintos de cero son de signo opuesto, y si no, de un cilindro elíptico cuando K es del signo de los valores propios distintos de cero, y l 'conjunto vacío de lo contrario.

Cuando el rango es igual a uno, solo un valor propio es distinto de cero, por ejemplo ; en un nuevo sistema de coordenadas ortonormal, la ecuación se convierte en: $\ beta ~$

\ beta y ^ 2 + px + qy = K ~~

luego, después de un último cambio de sistema de coordenadas ortonormal

\ beta y ^ 2 + P x = L ~~

Si P es cero, obtenemos un plano si L es cero, y la unión de dos planos o el conjunto vacío, dependiendo de si L es signo de o no. De lo contrario, es un cilindro parabólico. $\beta$

Clasificación en geometría afín

Clasificación en geometría proyectiva

Quadric en cualquier dimensión

De manera más general, en un espacio de dimensión D, si las coordenadas del espacio son , el cuadrático general es una hipersuperficie definida por la ecuación algebraica: $\ {x_1, x_2, \ dots, x_D \}$

\ sum_ {i, j = 1} ^ D Q_ {i, j} x_i x_j + \ sum_ {i = 1} ^ D P_i x_i + R = 0

para una elección específica de Q, P y R.

La ecuación normalizada para un cuadrático no degenerado centrado en el origen tiene la forma:

\ sum_ {i = 1} ^ D \ pm {x_i ^ 2 \ over a_i ^ 2} = 1

Aplicaciones

En modelado de imágenes

Para una superficie de ecuación , la fórmula de Taylor-Young proporciona una aproximación local de la superficie mediante la ecuación cuadrática: $z = f (x, y) ~$

p (xa) + q (yb) + \ frac {1} {2} [r (xa) ^ 2 + 2 s (xa) (yb) + t (yb) ^ 2]

con las llamadas notaciones Monge $p = \ frac {\ f parcial} {\ parcial x} (a, b), q = \ frac {\ parcial f} {\ parcial y} (a, b), r = \ frac {\ parcial ^ 2 f } {\ parcial x ^ 2} (a, b), t = \ frac {\ parcial ^ 2 f} {\ parcial y ^ 2} (a, b), s = \ frac {\ parcial ^ 2 f} { \ parcial x \ parcial y} (a, b).$

Esta aproximación local se utiliza en el modelado de imágenes, donde proporciona resultados interesantes.

Notas y referencias

André Warusfel , "Quadriques" , en Diccionario de matemáticas, álgebra, análisis, geometría , Encyclopædia Universalis y Albin Michel,1997.
Ni vacío, ni reducido a un punto, una línea, un plano o la unión de dos planos.
Sylvie Philipp, Modelado estructural de texturas. Extracción del grano primario y su regla de colocación en Duodécimo coloque Gretsi , Juan-les-Pins, 1988, Leer online , p. 590 .
Alaa Mustafa, Contribución al estudio de curvaturas discretas y sus aplicaciones , 2008 [Tesis].

Ver también

Cónico