Análisis espectral

En física y en diversas técnicas aparecen señales, funciones del tiempo o, más excepcionalmente, de una variable espacial. El análisis espectral incluye varias técnicas de descripción de estas señales en el dominio de la frecuencia. En particular, permite obtener las características de la respuesta de un sistema lineal utilizando una función de transferencia . En matemáticas, el análisis armónico es una parte de estas técnicas.

Presentación

Un fenómeno físico dependiente del tiempo se describe mediante una o más señales. Solo excepcionalmente podemos interpretarlos de manera simple. El problema es encontrar una descripción de su contenido, relativamente general y adaptada a los problemas concretos. Suelen aparecer de la siguiente manera: un sistema transforma una señal de entrada en una señal de salida, ¿cómo determinar las características de ésta según las de la señal de entrada y las del sistema?

En el caso general, lamentablemente no conocemos la relación entre los valores de la señal de salida y los de la señal de entrada, sino solo la relación entre las variaciones de la señal de salida y los valores (o posiblemente las variaciones) de la señal de entrada. En términos matemáticos , el sistema se rige por una ecuación diferencial . Si es así, el problema es insoluble.

Afortunadamente, existe una clase importante de sistemas, los sistemas lineales (o se supone que son tales) regidos por el principio de superposición. En este caso, correspondiente a una ecuación diferencial lineal, podemos intentar descomponer la señal de entrada en una suma de señales simples a las que podemos unir señales de salida igualmente simples cuya suma daría el resultado deseado.

El problema se simplifica aún más si las características del sistema se mantienen constantes en el tiempo. Se trata de una ecuación diferencial lineal con coeficientes constantes. Las señales simples son sinusoides que solo experimentan amplificación y desplazamiento de fase. Este es el problema del análisis espectral: descomponer una señal complicada en una suma de sinusoides.

Aquí surge una dificultad porque esta descomposición requiere que la señal se defina durante un tiempo infinito. Sin embargo, solo se puede conocer a través de un registro de duración limitada: por lo tanto, es necesario construir un modelo de la señal haciendo suposiciones, a menudo obvias intuitivamente, sobre la parte no registrada del fenómeno.

Diferentes modelos

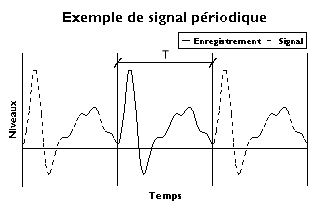
Se puede suponer, por ejemplo, que la señal reproduce indefinidamente el contenido de la grabación: luego se construye un modelo periódico basado en la serie de Fourier . La señal se describe mediante un espectro discreto (conjunto de frecuencias en progresión aritmética).

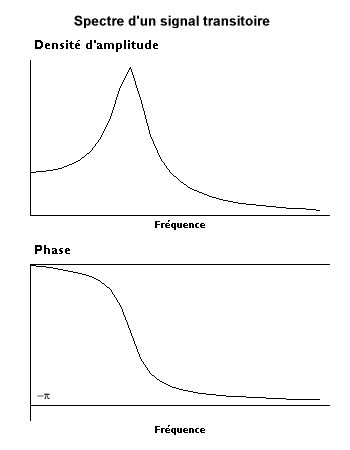
También podemos suponer que el nivel de la señal es despreciable fuera de la grabación: utilizamos en este caso un modelo transitorio basado en la transformación de Fourier que generalmente conduce a un espectro continuo.

Hay una serie de fenómenos naturales para los que ninguno de estos dos supuestos es realista. Por ejemplo, un registro de ondas, sin mostrar periodicidad, tampoco muestra una disminución neta sobre su duración relativamente pequeña: hablamos de una señal con varianza finita (algunos prefieren hablar de potencia finita pero todavía no es técnicamente relevante), lo que conduce a la noción de densidad espectral . Entonces podemos usar una suposición algo más difusa de que la raíz cuadrada media calculada en la grabación proporciona una estimación razonable de la raíz cuadrada media de la señal. Este tipo de análisis todavía conduce a un espectro continuo. Se define, como los anteriores, en base a la señal pero se puede obtener información adicional considerando ésta como una realización de un proceso aleatorio .

Señales periódicas

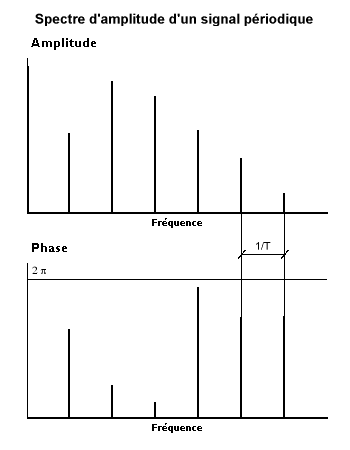
Espectro de amplitud de señal periódica.png

El desarrollo en serie de Fourier de un registro de duración asocia sinusoides de amplitudes finitas y frecuencias múltiples de la frecuencia fundamental . Estamos hablando de un espectro de amplitud que es un espectro de líneas. En el caso general, el resultado del análisis se puede expresar en amplitudes y fases, o en componentes coseno y seno. $T$ ${\ frac {1} {T}}$

La suma de las sinusoides crea una señal periódica. Si la señal original es periódica, está perfectamente representada, al menos en principio. De lo contrario, solo se ha mostrado la grabación y tienes que intentar encontrar otra cosa.

Señales transitorias

Espectro de densidad de amplitud de señal transitoria.png

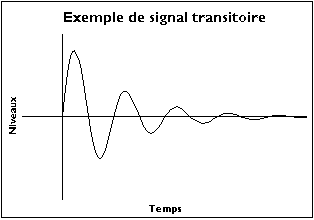
Aquí, en primer lugar, razonaremos sobre la señal de duración supuestamente infinita antes de ver las consecuencias de una grabación de duración finita. Si esta señal no es periódica, no tiene un período finito, podemos intentar ver qué pasaría si le dáramos un período infinito. Esto tiene las siguientes consecuencias:

Cuando el tiempo de análisis tiende hacia el infinito, el paso de frecuencia tiende hacia 0: en el límite, pasamos de un espectro discreto a un espectro continuo. $T$ ${\ frac {1} {T}}$
Durante este aumento en el período de análisis, cuando este último se multiplica por cualquier número n, el número de componentes se multiplica por el mismo factor. Para que el nivel de la señal no aumente en las mismas proporciones, las amplitudes de los componentes deben dividirse aproximadamente por n, lo que corre el riesgo de llevar a cero amplitudes en el límite. Esta dificultad se supera multiplicando los coeficientes de Fourier por la longitud del análisis o dividiéndolos por el paso de frecuencia que tiende a cero. Por tanto, el espectro continuo ya no es un espectro de amplitud sino un espectro de densidad de amplitud cuya unidad es unidad física / hercio.
A pesar de estas precauciones, el método puede diferir. Una condición de convergencia es que la señal debe ser transitoria: debe tender hacia 0 cuando el tiempo tiende hacia ± . $\ infty$

Obtenemos así la transformada de la señal que generalmente se indica , siendo f la frecuencia. $x (t)$ $X (f)$

Si vuelve a una grabación de tiempo limitado, hay dos posibilidades:

La señal es diferente de cero solo por un tiempo limitado: el análisis durante este tiempo proporciona, al menos en principio, un resultado exacto que permite reconstituir la señal por inversión de la transformación.
La señal tiene valores distintos de cero durante una duración superior a la del registro: la imprecisión del resultado aumenta con la cantidad de información perdida. El error así cometido se traduce concretamente por una dispersión de la energía correspondiente a una frecuencia en las frecuencias vecinas y matemáticamente por el concepto de convolución.

Señales de varianza finita

El problema es más complicado que en el caso anterior y se puede abordar de diversas formas. El que usaremos ciertamente no es el más eficiente desde el punto de vista científico pero tiene la ventaja de mostrar algunos puntos esenciales sin esconderlos detrás de consideraciones matemáticas, si no particularmente difícil, al menos bastante pesado. Para superar problemas específicos asociados con tener en cuenta un promedio distinto de cero, se supondrá que la señal se ha centrado de antemano restando su promedio.

Dada una señal , llamamos a la función de autocovarianza , a menudo asimilada erróneamente a la autocorrelación , cuya función da el promedio de los productos de los valores de en dos instantes que difieren de : $x (t)$ $\ tau$ $x (t)$ $\ tau$

R_ {x} (\ tau) = \ overline {x (t) x (t + \ tau)}

Al calcular esta media, t varía de a . Si la señal es transitoria, la función es cero; si es periódica, es en sí misma periódica. Al colocarse en el caso de una señal que obviamente no pertenece a ninguna de las dos categorías, la función tiene las siguientes propiedades: $- \ infty$ $+ \ infty$

El cambio de en no hace ninguna modificación: la función es par. $\ tau$ ${\ Displaystyle - \ tau}$
En el origen, representa la varianza que es necesariamente positiva. ${\ Displaystyle R_ {x} (0)}$
La simetría dicta que es un extremo. De hecho, se trata de un máximo: si en el cálculo se reemplaza el cambio 0 por un pequeño cambio , con cada cruce del nivel 0, se reemplaza un pequeño producto positivo por un pequeño producto negativo. $\ tau$
Con la excepción de la señal periódica, dos puntos separados por un gran desplazamiento tienen poco en común: la función tiende a 0 cuando este desplazamiento tiende a infinito. $\ tau$
Con todo, la función a menudo tiene una forma sinusoidal amortiguada y vaga.
Queremos, si es posible, asimilar la señal a una suma de sinusoides. Supongamos que este es el caso. Ya sea que las amplitudes sean finitas o infinitamente pequeñas, podemos escribir esta suma en la forma:

x (t) = \ sum _ {n} a_ {n} \ cos (\ omega _ {n} t + \ varphi _ {n})

Bajo estas condiciones mostramos que

R_ {x} (\ tau) = \ sum _ {n} {a_ {n} ^ {2} \ over 2} \ cos {\ omega _ {n} \ tau}

Entonces

La función de autocovarianza contiene las mismas frecuencias que la señal.
Las amplitudes no son idénticas pero se obtienen elevando al cuadrado y dividiendo por 2.
Las fases han desaparecido por completo: la autocovarianza corresponde no solo a la señal original, sino también a todas aquellas que contienen los mismos componentes.

Densidad espectral

Podemos deducir de lo anterior:

La función de autocovarianza tiene una transformada de Fourier que llamamos densidad espectral y que generalmente denotamos , siendo f la frecuencia. ${\ Displaystyle S_ {x} (f)}$
Dado que los componentes de la autocovarianza son homogéneos a los cuadrados de amplitud, la densidad espectral no es negativa. Tiene una dimensión (unidad física) 2 / Hertz.
Siendo la autocovarianza una función real y uniforme, su transformada de Fourier tiene las mismas características.
Una grabación siempre trunca la señal que se supone que se mantiene durante un tiempo infinito, la densidad espectral está necesariamente distorsionada por convolución.

Relación con procesos aleatorios

Además de la distorsión del contenido de frecuencia ya observada para señales transitorias, existe una incertidumbre estadística relacionada con la posición de la grabación en la señal.

La función de autocovarianza corresponde a toda una familia de señales que contienen los mismos componentes. Esta familia se puede interpretar como la de los logros de un proceso continuo . Una grabación por tiempo limitado también puede verse como un logro de otro proceso. Esto permite especificar con intervalos de confianza el valor estadístico del análisis realizado.

Ver también

Bibliografía

(en) YK Lin , Teoría probabilística de la dinámica estructural , Nueva York, Robert E. Krieger Publishing Company,Julio de 1976, 368 p. ( ISBN 0-88275-377-0 )