Algoritmo de gráfico de segmento de Bresenham

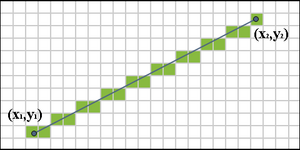
El algoritmo de gráfico de segmentos de Bresenham es un algoritmo desarrollado por Jack E. Bresenham enMayo de 1962, mientras trabajaba en un laboratorio de computación de IBM y buscaba pilotar un trazador conectado a una consola de texto. Este algoritmo se presentó en la convención ACM en 1963 y luego se publicó en 1965 en IBM Systems Journal .

El algoritmo determina qué puntos de un plano discreto deben trazarse para formar una aproximación de segmento de línea entre dos puntos dados. Este algoritmo se usa a menudo para dibujar segmentos de línea en una pantalla de computadora o una imagen calculada para imprimir. Se considera uno de los primeros algoritmos descubiertos en el campo de la síntesis de imágenes .

Usos

El principio de cálculo está ampliamente documentado y desde entonces se ha utilizado para trazar incrementalmente cualquier curva cónica ( círculo , elipse , arco , parábola , hipérbola ) o curvas de Bézier gracias a las propiedades de su función polinomial de definición, cuyas derivadas hacen posible. para calcular las orientaciones de segmentos elementales con operaciones simples con enteros. Incluso se puede adaptar a la aproximación de curvas de las que se conoce solo un desarrollo limitado (de las cuales se tomarán solo los primeros términos de grado débil), utilizables con una buena precisión en un campo suficiente en comparación con la resolución ( sinusoides , exponenciales , potencias no enteras).

El algoritmo también es fácilmente adaptable al cálculo de curvas y superficies en un espacio discreto de más de 2 dimensiones (en particular para el control de máquinas herramienta). Incluso en solo dos dimensiones, podemos discretizar con este algoritmo una curva con función de suavizado teniendo en cuenta el error cometido entre dos puntos candidatos para ajustar su color, siendo convertible el error incremental en un coeficiente de transparencia, que mantiene la grasa ( espesor visual) de una curva mientras se limita el efecto de escalera ( aliasing ).

Este algoritmo también se utiliza para suavizar representaciones de texturas 2D aplicadas a superficies de una escena 3D donde la textura se reduce o aumenta. También se utiliza para suavizar ampliaciones fotográficas o para interpolar colores intermedios en una escala discreta.

Explicación del algoritmo básico en el primer octante

La línea se traza entre dos puntos ( x 1 , y 1 ) y ( x 2 , y 2 ), donde cada par indica la columna y la fila, respectivamente, aumentando hacia la derecha y hacia abajo. Inicialmente asumiremos que nuestro segmento desciende hacia abajo y hacia la derecha, y que la distancia horizontal x 2 - x 1 excede la distancia vertical y 2 - y 1 (es decir, el segmento tiene una pendiente entre 0 y -1). Nuestro objetivo es, para cada columna x entre x 1 y x 2 , identificar la fila y en esa columna que está más cerca del segmento ideal y trazar un píxel en ( x , y ).

Determinación de ordenadas

Ahora es cuestión de determinar qué píxel está más cerca de la línea para una columna determinada. La fórmula general de una línea entre los dos puntos viene dada por:

y-y_ {1} = {\ frac {y_ {2} -y_ {1}} {x_ {2} -x_ {1}}} \ cdot \ left (x-x_ {1} \ right)

. (1)

Como se conoce la columna , la fila del píxel más cercana a la ordenada exacta del punto de abscisas en la línea se obtiene redondeando esta ordenada $y$ al número entero más cercano: $\ dot {x}$ ${\ dot {y}}$ $x = {\ dot {x}}$

{\ dot {y}} = \ left \ lfloor {\ frac {y_ {2} -y_ {1}} {x_ {2} -x_ {1}}} \ cdot \ left ({\ dot {x}} -x_ {1} \ right) + y_ {1} +0.5 \ right \ rfloor

. (2)

El valor 0.5 en el lado derecho es una aproximación de las coordenadas (el punto está en el medio del cuadrado).

Sin embargo, calcular este valor explícitamente para cada columna es caro. Sin embargo, comenzamos en , y cada vez que agregamos 1 a la abscisa, agregamos el valor constante al valor de la ordenada $y$ del punto de la línea correspondiente. Este valor es la pendiente de la línea y, según nuestra suposición inicial, está entre 0 y -1. Después de redondear, para cada columna , usamos el valor anterior (ordenada del píxel de abscisas ) o este valor aumentado en 1. $\ dot {x}$ $\ left ({\ dot {x}}, {\ dot {y}} \ right)$ $(x_ {1}, y_ {1}) \$ $e _ {{(1,0)}} = {\ frac {y_ {2} -y_ {1}} {x_ {2} -x_ {1}}}$ $\ dot {x}$ ${\ dot {y}}$ ${\ dot {x}} - 1$

Podemos decidir cuál de estos dos valores para tomar por mantener un valor de error que representa la distancia vertical entre el actual valor y la exacta $y$ el valor de la línea en el actual eje de abscisas . Al principio, este valor de error e es cero y cada vez que incrementamos , aumentamos el valor de error por el valor de pendiente anterior. Cada vez que el error excede 0.5, la línea se acerca al siguiente valor , por lo que sumamos 1 a mientras que simultáneamente restamos 1.0 al error e . ${\ dot {y}}$ $x = {\ dot {x}}$ $\ dot {x}$ ${\ dot {y}}$ ${\ dot {y}}$

El procedimiento se ve así, asumiendo que es una primitiva gráfica que traza el píxel de la fila xy la columna $y$ ; expresado en pseudocódigo , el algoritmo básico es: tracerPixel(x, y)

procédure tracerSegment(entier x1, entier y1, entier x2, entier y2) est déclarer entier x, y, dx, dy ; déclarer rationnel e, e(1,0), e(0,1) ; // valeur d’erreur et incréments dy ← y2 - y1 ; dx ← x2 - x1 ; y ← y1 ; // rangée initiale e ← 0,0 ; // valeur d’erreur initiale e(1,0) ← dy / dx ; e(0,1) ← -1.0 ; pour x variant de x1jusqu’à x2par incrément de 1 faire tracerPixel(x, y) ; si (e ← e + e(1,0)) ≥ 0,5 alors // erreur pour le pixel suivant de même rangée y ← y + 1 ; // choisir plutôt le pixel suivant dans la rangée supérieure e ← e + e(0,1) ; // ajuste l’erreur commise dans cette nouvelle rangée fin si ; fin pour ; fin procédure ;

Mejora del algoritmo para el cálculo con enteros

El problema con este sencillo algoritmo es que los microprocesadores son relativamente lentas en el cálculo sobre números de punto (y la representación se ha sugerido anteriormente como números racionales para flotante e y e (1,0) es significativamente más complejo y no es compatible de forma nativa por los procesadores que aumenta el número de instrucciones para trabajar con tales números); además, los errores de aproximación del número de coma flotante e (1.0) se acumulan con cada adición de e (1.0) en e . Trabajar solo con números enteros permitiría un cálculo más exacto y rápido.

El primer truco es notar primero que podemos reemplazar e por e –0.5, lo que permite probar solo el signo del valor de error en lugar de comparar dos fundamentos, la prueba de proximidad con respecto a la línea exacta luego se reduce a saber cuál de los dos píxeles candidatos se encuentra debajo de la línea paralela exacta cuyas ordenadas se incrementan en 0.5, y para reemplazar el redondeo de la fórmula (1) anterior con el número entero más cercano redondeando a un número entero igual o menor con esta nueva línea, que efectivamente no cambia la fórmula (2) anterior, pero e representará el error cometido durante la aproximación de esta segunda línea por los píxeles trazados:

procédure tracerSegment(entier x1, entier y1, entier x2, entier y2) est déclarer entier x, y, dx, dy ; déclarer rationnel e, e(1,0), e(0,1) ; // valeur d’erreur et incréments dy ← y2 - y1 ; dx ← x2 - x1 ; y ← y1 ; // rangée initiale e ← -0,5 ; // valeur d’erreur initiale e(1,0) ← dy / dx ; e(0,1) ← -1.0 ; pour x variant de x1jusqu’à x2par incrément de 1 faire tracerPixel(x, y) ; si (e ← e + e(1,0)) ≥ 0 alors // erreur pour le pixel suivant de même rangée y ← y + 1 ; // choisir plutôt le pixel suivant dans la rangée supérieure e ← e + e(0,1) ; // ajuste l’erreur commise dans cette nouvelle rangée fin si ; fin pour ; fin procédure ;

Luego, al multiplicar todos los fundamentos anteriores por dx , el cálculo ya no requiere incrementos racionales (lo que elimina la acumulación de errores de aproximación de los flotantes). Sin embargo, el valor inicial de e = –0,5 × dx aún no es entero, aunque sus incrementos sean enteros.

procédure tracerSegment(entier x1, entier y1, entier x2, entier y2) est déclarer entier x, y, dx, dy ; déclarer rationnel e ; // valeur d’erreur déclarer entier e(1,0), e(0,1) ; // incréments dy ← y2 - y1 ; dx ← x2 - x1 ; y ← y1 ; // rangée initiale e ← -0,5 × dx ; // valeur d’erreur initiale e(1,0) ← dy ; e(0,1) ← -dx ; pour x variant de x1jusqu’à x2par incrément de 1 faire tracerPixel(x, y) ; si (e ← e + e(1,0)) ≥ 0 alors // erreur pour le pixel suivant de même rangée y ← y + 1 ; // choisir plutôt le pixel suivant dans la rangée supérieure e ← e + e(0,1) ; // ajuste l’erreur commise dans cette nouvelle rangée fin si ; fin pour ; fin procédure ;

Sin embargo, al duplicar e (y los valores de sus incrementos), esto no cambia nada al probar su signo: e entonces representará la distancia desde la línea exacta de ordenadas aumentada en 0.5, esta distancia se multiplica por la constante del factor positivo 2 × dy (que no cambia el signo del valor de error probado). El valor de pendiente utilizado como un incremento de e también se multiplica por el mismo factor simplemente se convierte en 2 × dy , su valor inicial se convierte en - dx , el segundo decremento condicional se convierte en 2 × dx (que también se puede calcular previamente). Entonces, el algoritmo se convierte en:

procédure tracerSegment(entier x1, entier y1, entier x2, entier y2) est déclarer entier x, y, dx, dy ; déclarer entier e ; // valeur d’erreur déclarer entier e(1,0), e(0,1) ; // incréments dy ← y2 - y1 ; dx ← x2 - x1 ; y ← y1 ; // rangée initiale e ← -dx ; // valeur d’erreur initiale e(1,0) ← dy × 2 ; e(0,1) ← -dx × 2; pour x variant de x1jusqu’à x2par incrément de 1 faire tracerPixel(x, y) ; si (e ← e + e(1,0)) ≥ 0 alors // erreur pour le pixel suivant de même rangée y ← y + 1 ; // choisir plutôt le pixel suivant dans la rangée supérieure e ← e + e(0,1) ; // ajuste l’erreur commise dans cette nouvelle rangée fin si ; fin pour ; fin procédure ;

Reducción de variables y simplificaciones

Finalmente, podemos cambiar el signo de e probando el signo opuesto, luego reducir el número de variables, notando que x1 e y1 anteriores ya no se usan tan pronto como se calculan el error inicial y los incrementos; basta con cambiar también el signo de los incrementos y decrementos:

procédure tracerSegment(entier x1, entier y1, entier x2, entier y2) est déclarer entier dx, dy ; déclarer entier e ; // valeur d’erreur e ← x2 - x1 ; // -e(0,1) dx ← e × 2 ; // -e(0,1) dy ← (y2 - y1) × 2 ; // e(1,0) tant que x1 ≤ x2faire tracerPixel(x1, y1) ; x1 ← x1 + 1 ; // colonne du pixel suivant si (e ← e - dy) ≤ 0 alors // erreur pour le pixel suivant de même rangée y1 ← y1 + 1 ; // choisir plutôt le pixel suivant dans la rangée supérieure e ← e + dx ; // ajuste l’erreur commise dans cette nouvelle rangée fin si ; fin faire ; // Le pixel final (x2, y2) n’est pas tracé. fin procédure ;

Este algoritmo es óptimo y suficiente para trazar cualquier vector horizontal diagonal u oblicuo en el primer octante, de columnas y filas crecientes. Si el lenguaje de programación lo permite, las dos variables locales declaradas X e Y pueden ser reemplazados por la reutilización de las variables x 1 y y 1 de los parámetros. Este caso se trata más arriba.

Sin embargo, debe tenerse en cuenta en el algoritmo anterior que la prueba del signo de e también puede incluir la igualdad con cero o no incluirlo. Esto corresponde al hecho de que los siguientes dos píxeles candidatos son equidistantes de la línea exacta. Si elegimos un desplazamiento diagonal, el segundo punto siguiente siempre se obtendrá mediante un desplazamiento horizontal; si se elige un desplazamiento horizontal, el segundo punto siguiente siempre se obtendrá mediante un desplazamiento diagonal. Si invirtiéramos la dirección del vector, los píxeles elegidos estarían invertidos y por tanto diferentes, y tendremos que tener esto en cuenta si queremos una superposición exacta de los píxeles de dos vectores oblicuos de direcciones opuestas, al generalizar el algoritmo a vectores oblicuos en cualquier dirección (esto no puede ocurrir al dibujar vectores horizontales, verticales o diagonales).

Algoritmo general optimizado

La generalización del algoritmo básico a la gráfica de vectores de cualquier dirección se obtiene mediante simetría simple.

El algoritmo se desarrolla y optimiza aquí en cada uno de los ocho octantes. Sin embargo, para asegurar que siempre se dibujarán los mismos píxeles para dos vectores idénticos pero de dirección opuesta, revertiremos los casos límite donde un desplazamiento diagonal es igual a un desplazamiento a la derecha, eligiendo la diagonal cuando el vector está orientado hacia la izquierda (coordenadas x decrecientes) en lugar de la derecha (coordenadas x crecientes) como en el caso simplificado anterior:

procédure tracerSegment(entier x1, entier y1, entier x2, entier y2) est déclarer entier dx, dy; si (dx ← x2 - x1) ≠ 0 alors si dx > 0 alors si (dy ← y2 - y1) ≠ 0 alors si dy > 0 alors // vecteur oblique dans le 1er cadran si dx ≥ dy alors // vecteur diagonal ou oblique proche de l’horizontale, dans le 1er octant déclarer entier e ; dx ← (e ← dx) × 2 ; dy ← dy × 2 ; // e est positif boucle sans fin // déplacements horizontaux tracePixel(x1, y1) ; interrompre boucle si (x1 ← x1 + 1) = x2 ; si (e ← e - dy) < 0 alors y1 ← y1 + 1 ; // déplacement diagonal e ← e + dx ; fin si ; fin boucle ; sinon // vecteur oblique proche de la verticale, dans le 2d octant déclarer entier e ; dy ← (e ← dy) × 2 ; dx ← dx × 2 ; // e est positif boucle sans fin // déplacements verticaux tracePixel(x1, y1) ; interrompre boucle si (y1 ← y1 + 1) = y2 ; si (e ← e - dx) < 0 alors x1 ← x1 + 1 ; // déplacement diagonal e ← e + dy ; fin si ; fin boucle ; fin si ; sinon // dy < 0 (et dx > 0) // vecteur oblique dans le 4e cadran si dx ≥ -dy alors // vecteur diagonal ou oblique proche de l’horizontale, dans le 8e octant déclarer entier e ; dx ← (e ← dx) × 2 ; dy ← dy × 2 ; // e est positif boucle sans fin // déplacements horizontaux tracePixel(x1, y1) ; interrompre boucle si (x1 ← x1 + 1) = x2 ; si (e ← e + dy) < 0 alors y1 ← y1 - 1 ; // déplacement diagonal e ← e + dx ; fin si ; fin boucle ; sinon // vecteur oblique proche de la verticale, dans le 7e octant déclarer entier e ; dy ← (e ← dy) × 2 ; dx ← dx × 2 ; // e est négatif boucle sans fin // déplacements verticaux tracePixel(x1, y1) ; interrompre boucle si (y1 ← y1 - 1) = y2 ; si (e ← e + dx) > 0 alors x1 ← x1 + 1 ; // déplacement diagonal e ← e + dy ; fin si ; fin boucle ; fin si ; fin si ; sinon // dy = 0 (et dx > 0) // vecteur horizontal vers la droite répéter tracePixel(x1, y1) ; jusqu’à ce que (x1 ← x1 + 1) = x2 ; fin si ; sinon // dx < 0 si (dy ← y2 - y1) ≠ 0 alors si dy > 0 alors // vecteur oblique dans le 2d cadran si -dx ≥ dy alors // vecteur diagonal ou oblique proche de l’horizontale, dans le 4e octant déclarer entier e ; dx ← (e ← dx) × 2 ; dy ← dy × 2 ; // e est négatif boucle sans fin // déplacements horizontaux tracePixel(x1, y1) ; interrompre boucle si (x1 ← x1 - 1) = x2 ; si (e ← e + dy) ≥ 0 alors y1 ← y1 + 1 ; // déplacement diagonal e ← e + dx ; fin si ; fin boucle ; sinon // vecteur oblique proche de la verticale, dans le 3e octant déclarer entier e ; dy ← (e ← dy) × 2 ; dx ← dx × 2 ; // e est positif boucle sans fin // déplacements verticaux tracePixel(x1, y1) ; interrompre boucle si (y1 ← y1 + 1) = y2 ; si (e ← e + dx) ≤ 0 alors x1 ← x1 - 1 ; // déplacement diagonal e ← e + dy ; fin si ; fin boucle ; fin si ; sinon // dy < 0 (et dx < 0) // vecteur oblique dans le 3e cadran si dx ≤ dy alors // vecteur diagonal ou oblique proche de l’horizontale, dans le 5e octant déclarer entier e ; dx ← (e ← dx) × 2 ; dy ← dy × 2 ; // e est négatif boucle sans fin // déplacements horizontaux tracePixel(x1, y1) ; interrompre boucle si (x1 ← x1 - 1) = x2 ; si (e ← e - dy) ≥ 0 alors y1 ← y1 - 1 ; // déplacement diagonal e ← e + dx ; fin si ; fin boucle ; sinon // vecteur oblique proche de la verticale, dans le 6e octant déclarer entier e ; dy ← (e ← dy) × 2 ; dx ← dx × 2 ; // e est négatif boucle sans fin // déplacements verticaux tracePixel(x1, y1) ; interrompre boucle si (y1 ← y1 - 1) = y2 ; si (e ← e - dx) ≥ 0 alors x1 ← x1 - 1 ; // déplacement diagonal e ← e + dy ; fin si ; fin boucle ; fin si ; fin si ; sinon // dy = 0 (et dx < 0) // vecteur horizontal vers la gauche répéter tracePixel(x1, y1) ; jusqu’à ce que (x1 ← x1 - 1) = x2 ; fin si ; fin si ; sinon // dx = 0 si (dy ← y2 - y1) ≠ 0 alors si dy > 0 alors // vecteur vertical croissant répéter tracePixel(x1, y1) ; jusqu’à ce que (y1 ← y1 + 1) = y2 ; sinon // dy < 0 (et dx = 0) // vecteur vertical décroissant répéter tracePixel(x1, y1) ; jusqu’à ce que (y1 ← y1 - 1) = y2 ; fin si ; fin si ; fin si ; // le pixel final (x2, y2) n’est pas tracé. fin procédure ;

Notas:

Arriba, las asignaciones a veces se agrupan dentro de expresiones que reutilizan el valor asignado. Si el lenguaje utilizado no lo permite, basta con realizar las asignaciones internas en instrucciones de asignación previa separadas, y releer esta variable en la expresión contenedora.
Las primitivas gráficas tracePixel ( x 1 , y 1 ) se agrupan arriba para dibujar segmentos horizontales (caso del primer octante arriba) o verticales (segundo octante) en el bucle interno, y se pueden agrupar en una sola llamada (basta para contar el número de pasajes en el bucle interno, y para dibujar el trazo del segmento horizontal (o vertical) a la salida de este bucle.

Referencias

James D. Foley, Introducción a los gráficos por computadora , París, Addison-Wesley Francia,Mayo de 1995, 573 p. ( ISBN 978-2-87908-058-1 , aviso BnF n o FRBNF37480856 ) , páginas 76 a 84

(en) Jack E. Bresenham , “ Algoritmo para el control por computadora de un trazador digital ” , IBM Systems Journal , vol. 4, n o 1,1 st 01 1965, p. 25–30 ( DOI 10.1147 / sj.41.0025 , leer en línea )