Triángulo heptagonal

En geometría , el triángulo heptagonal es el triángulo , único salvo similitud , de ángulos de medidas en radianes $π / 7$ , $2π / 7$ y $4π / 7$ , es decir aproximadamente 26 °, 51 ° y 103 °. Es el único triángulo cuyos ángulos están en proporciones de 4: 2: 1.

Se obtiene en el heptágono convexo regular partiendo de uno de los vértices y tomando el segundo y cuarto vértices. Por lo tanto, sus lados están formados por un lado del heptágono regular y dos de sus diagonales (una larga y otra corta).

Como el triángulo áureo , cuyos ángulos están en las proporciones 2: 2: 1, el triángulo heptagonal tiene muchas propiedades notables.

El triángulo heptagonal y sus centros

El centro del círculo de Euler del triángulo heptagonal es también su primer punto de Brocard . El segundo punto de Brocard está en el círculo de Euler.

El centro del círculo circunscrito y los puntos de Fermat del triángulo heptagonal forman un triángulo equilátero .

Al denotar $R$ el radio del círculo circunscrito y $r$ el centro del círculo inscrito , podemos expresar la distancia entre el centro del círculo circunscrito O y el ortocentro H por

{\ Displaystyle OH = R {\ sqrt {2}},}

y la distancia entre el centro del círculo circunscrito I en el ortocentro por

{\ Displaystyle IH ^ {2} = {\ frac {R ^ {2} + 4r ^ {2}} {2}}.}

Las dos tangentes al círculo circunscrito que resultan del ortocentro son perpendiculares .

Relaciones entre distancias

Longitudes de los lados

Los lados del triángulo heptagonal $a < b < c$ coinciden, por definición, con el lado del heptágono regular, su diagonal corta y su diagonal larga. Estas tres longitudes verifican

{\ Displaystyle a ^ {2} = c (cb), \ b ^ {2} = a (c + a), \ c ^ {2} = b (a + b), \ {\ frac {1} { a}} = {\ frac {1} {b}} + {\ frac {1} {c}}}

(este último se conoce como la ecuación óptica (en) ) y por lo tanto

{\ Displaystyle ab + ac = bc,}

{\ Displaystyle b ^ {3} + 2b ^ {2} c-bc ^ {2} -c ^ {3} = 0,}

{\ Displaystyle c ^ {3} -2c ^ {2} a-ca ^ {2} + a ^ {3} = 0,}

{\ Displaystyle a ^ {3} -2a ^ {2} b-ab ^ {2} + b ^ {3} = 0.}

Por lo tanto, las razones $- b / c$ , $c / a$ y $a / b$ son las raíces de la ecuación cúbica.

{\ Displaystyle t ^ {3} -2t ^ {2} -t + 1 = 0.}

No existe una expresión algebraica real para las soluciones de esta ecuación, ya que es un ejemplo de casus irreducibilis . Sin embargo, tenemos las aproximaciones

{\ Displaystyle b \ approx 1,80193 \ cdot a, \ qquad c \ approx 2,24698 \ cdot a.}

También tenemos

{\ Displaystyle {\ frac {a ^ {2}} {bc}}, \ quad - {\ frac {b ^ {2}} {ca}}, \ quad - {\ frac {c ^ {2}} { ab}}}

que verifican la ecuación cúbica

{\ Displaystyle t ^ {3} + 4t ^ {2} + 3t-1 = 0.}

Se tiene

{\ Displaystyle {\ frac {a ^ {3}} {bc ^ {2}}}, \ quad - {\ frac {b ^ {3}} {ca ^ {2}}}, \ quad {\ frac { c ^ {3}} {ab ^ {2}}}}

que verifican la ecuación cúbica

{\ Displaystyle t ^ {3} -t ^ {2} -9t + 1 = 0.}

Se tiene

{\ Displaystyle {\ frac {a ^ {3}} {b ^ {2} c}}, \ quad {\ frac {b ^ {3}} {c ^ {2} a}}, \ quad - {\ frac {c ^ {3}} {a ^ {2} b}}}

que verifican la ecuación cúbica

{\ Displaystyle t ^ {3} + 5t ^ {2} -8t + 1 = 0.}

Se tiene

{\ Displaystyle b ^ {2} -a ^ {2} = ac, \ c ^ {2} -b ^ {2} = ab, \ a ^ {2} -c ^ {2} = - bc,}

{\ Displaystyle {\ frac {b ^ {2}} {a ^ {2}}} + {\ frac {c ^ {2}} {b ^ {2}}} + {\ frac {a ^ {2} } {c ^ {2}}} = 5.}

También tenemos

{\ Displaystyle ab-bc + ca = 0,}

{\ Displaystyle a ^ {3} bb ^ {3} c + c ^ {3} a = 0,}

{\ Displaystyle a ^ {4} b + b ^ {4} cc ^ {4} a = 0,}

{\ Displaystyle a ^ {11} b ^ {3} -b ^ {11} c ^ {3} + c ^ {11} a ^ {3} = 0.}

No hay otro par de enteros estrictamente positivos ( m , n ), m , n > 0, m, n <2000 tal que

{\ Displaystyle a ^ {m} b ^ {n} \ pm b ^ {m} c ^ {n} \ pm c ^ {m} a ^ {n} = 0.}

Alturas

Las alturas $h a$ , $h b$ y $h c$ verifican

{\ Displaystyle h_ {a} = h_ {b} + h_ {c}}

{\ Displaystyle h_ {a} ^ {2} + h_ {b} ^ {2} + h_ {c} ^ {2} = {\ frac {a ^ {2} + b ^ {2} + c ^ {2 }} {2}}}

La altura del lado b (del ángulo opuesto B ) es la mitad de la bisectriz interna $w A$ de A :

{\ Displaystyle 2h_ {b} = w_ {A}.}

Aquí, el ángulo A es el ángulo más pequeño y B el segundo más pequeño.

Bisectrices internas

Las longitudes de las bisectrices internas $w A$ , $w B$ y $w C$ (bisectrices de los ángulos A , B y C respectivamente) verifican:

{\ Displaystyle w_ {A} = b + c, \ w_ {B} = ca, w_ {C} = ba.}

Rayos de círculos circunscritos, inscritos y exinscritos

Denotamos por $R$ el radio del círculo circunscrito al triángulo heptagonal. Su área vale entonces:

{\ Displaystyle A = {\ frac {\ sqrt {7}} {4}} R ^ {2}.}

También tenemos

{\ Displaystyle a ^ {2} + b ^ {2} + c ^ {2} = 7R ^ {2}, \ quad a ^ {4} + b ^ {4} + c ^ {4} = 21R ^ { 4}, \ quad a ^ {6} + b ^ {6} + c ^ {6} = 70R ^ {6},}

{\ Displaystyle {\ frac {1} {a ^ {2}}} + {\ frac {1} {b ^ {2}}} + {\ frac {1} {c ^ {2}}} = {\ frac {2} {R ^ {2}}}, \ quad {\ frac {1} {a ^ {4}}} + {\ frac {1} {b ^ {4}}} + {\ frac {1 } {c ^ {4}}} = {\ frac {2} {R ^ {4}}}, \ quad {\ frac {1} {a ^ {6}}} + {\ frac {1} {b ^ {6}}} + {\ frac {1} {c ^ {6}}} = {\ frac {17} {7R ^ {6}}}.}

En general, para cualquier número entero n ,

{\ Displaystyle a ^ {2n} + b ^ {2n} + c ^ {2n} = g (n) (2R) ^ {2n}}

con

{\ Displaystyle g (-1) = 8, \ quad g (0) = 3, \ quad g (1) = 7}

{\ Displaystyle g (n) = 7g (n-1) -14g (n-2) + 7g (n-3),}

se tiene

{\ Displaystyle 2b ^ {2} -a ^ {2} = {\ sqrt {7}} bR, \ quad 2c ^ {2} -b ^ {2} = {\ sqrt {7}} cR, \ quad 2a ^ {2} -c ^ {2} = - {\ sqrt {7}} aR.}

También tenemos

{\ Displaystyle a ^ {3} c + b ^ {3} ac ^ {3} b = -7R ^ {4},}

{\ Displaystyle a ^ {4} cb ^ {4} a + c ^ {4} b = 7 {\ sqrt {7}} R ^ {5},}

{\ Displaystyle a ^ {11} c ^ {3} + b ^ {11} a ^ {3} -c ^ {11} b ^ {3} = - 7 ^ {3} 17R ^ {14}.}

La razón $r / R$ entre el radio del círculo inscrito y el del círculo circunscrito es la raíz positiva de la ecuación cúbica

{\ Displaystyle 8x ^ {3} + 28x ^ {2} + 14x-7 = 0.}

El radio del círculo descrito en el lado $a$ es igual al radio del círculo de Euler del triángulo heptagonal.

Triángulo órtico

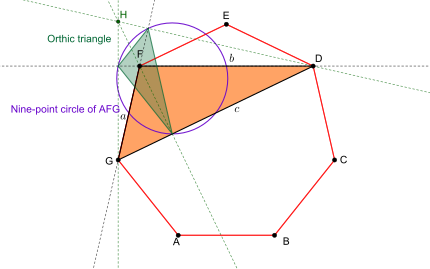
El triángulo órtico del triángulo heptagonal, cuyos vértices son los pies de las alturas , es similar al triángulo heptagonal, en la proporción 1 ⁄ 2 . El triángulo heptagonal es el único triángulo obtuso que es similar a su triángulo órtico (el triángulo equilátero es el único triángulo acutangular con la misma propiedad y con la misma razón de proporcionalidad).

El círculo circunscrito al triángulo órtico del triángulo heptagonal es el círculo de Euler del triángulo heptagonal.

Trigonometría

Las muchas identidades trigonométricas asociadas con el triángulo heptagonal incluyen

{\ Displaystyle A = {\ frac {\ pi} {7}}, \ quad B = {\ frac {2 \ pi} {7}} = 2A, \ quad C = {\ frac {4 \ pi} {7 }} = 4A = 2B}

{\ Displaystyle \ cos A = {\ frac {b} {2a}}, \ quad \ cos B = {\ frac {c} {2b}}, \ quad \ cos C = - {\ frac {a} {2c }},}

{\ Displaystyle \ cos A \ cos B \ cos C = - {\ frac {1} {8}}.}

Demostración

Aplicamos la ley de los senos al triángulo heptagonal:

{\ Displaystyle {\ frac {a} {\ sin (A)}} = {\ frac {b} {\ sin (B)}} = {\ frac {c} {\ sin (C)}} = 2R}

Por otro lado, el valor de los ángulos da:

{\ Displaystyle \ sin (4A) = \ sin (3A) \ Longrightarrow \ cos ^ {2} (A) - \ cos (A) \ cos (2A) = {\ frac {1} {4}}, \ sin (A) = \ sin (6A), \ cos (C) = - \ cos (3A).}

Entonces tenemos :

{\ Displaystyle {\ frac {b} {a}} = {\ frac {\ sin (2B)} {\ sin (A)}} = 2 \ cos (A), \ {\ frac {c} {b} } = {\ frac {\ sin (2B)} {\ sin (B)}} = 2 \ cos (B), \ quad {\ frac {a} {c}} = {\ frac {\ sin (A) } {\ sin (C)}} = {\ frac {\ sin (6A)} {\ sin (3A)}} = 2 \ cos (3A) = - 2 \ cos (C).}

El producto de estas tres identidades da:

{\ Displaystyle \ cos A \ cos B \ cos C = {\ frac {b} {2a}} \ times {\ frac {c} {2b}} \ times \ left (- {\ frac {a} {c} } \ right) = - {\ frac {1} {8}}.}

Por diferentes métodos (como el uso juicioso de la fórmula de Moivre ), podemos encontrar las siguientes igualdades:

{\ Displaystyle \ cos ^ {2} A + \ cos ^ {2} B + \ cos ^ {2} C = {\ frac {5} {4}},}

{\ Displaystyle \ cos ^ {4} A + \ cos ^ {4} B + \ cos ^ {4} C = {\ frac {13} {16}},}

{\ Displaystyle \ cot A + \ cot B + \ cot C = {\ sqrt {7}},}

{\ Displaystyle \ cot ^ {2} A + \ cot ^ {2} B + \ cot ^ {2} C = 5,}

{\ Displaystyle \ csc ^ {2} A + \ csc ^ {2} B + \ csc ^ {2} C = 8,}

{\ Displaystyle \ csc ^ {4} A + \ csc ^ {4} B + \ csc ^ {4} C = 32,}

{\ Displaystyle \ sec ^ {2} A + \ sec ^ {2} B + \ sec ^ {2} C = 24,}

{\ Displaystyle \ sec ^ {4} A + \ sec ^ {4} B + \ sec ^ {4} C = 416,}

{\ Displaystyle \ sin A \ sin B \ sin C = {\ frac {\ sqrt {7}} {8}},}

{\ Displaystyle \ sin ^ {2} A \ sin ^ {2} B \ sin ^ {2} C = {\ frac {7} {64}},}

{\ Displaystyle \ sin ^ {2} A + \ sin ^ {2} B + \ sin ^ {2} C = {\ frac {7} {4}},}

{\ Displaystyle \ sin ^ {4} A + \ sin ^ {4} B + \ sin ^ {4} C = {\ frac {21} {16}},}

{\ Displaystyle \ tan A \ tan B \ tan C = \ tan A + \ tan B + \ tan C = - {\ sqrt {7}},}

{\ Displaystyle \ tan ^ {2} A + \ tan ^ {2} B + \ tan ^ {2} C = 21.}

La raíz positiva de la ecuación cúbica

{\ Displaystyle x ^ {3} + x ^ {2} -2x-1 = 0}

Igual ${\ Displaystyle 2 \ cos {\ frac {2 \ pi} {7}}.}$

Con los senos nasales

Las raíces de la ecuación cúbica

{\ Displaystyle x ^ {3} - {\ frac {\ sqrt {7}} {2}} x ^ {2} + {\ frac {\ sqrt {7}} {8}} = 0}

están ${\ Displaystyle \ sin \ left ({\ frac {2 \ pi} {7}} \ right), \ sin \ left ({\ frac {4 \ pi} {7}} \ right), \ sin \ left ( {\ frac {8 \ pi} {7}} \ right).}$

Las raíces de la ecuación cúbica

{\ displaystyle 64y ^ {3} -112y ^ {2} + 56y-7 = 0}

están ${\ Displaystyle \ sin ^ {2} \ left ({\ frac {\ pi} {7}} \ right), \ sin ^ {2} \ left ({\ frac {2 \ pi} {7}} \ right ), \ sin ^ {2} \ left ({\ frac {4 \ pi} {7}} \ right).}$

También tenemos :

{\ Displaystyle \ sin A- \ sin B- \ sin C = - {\ frac {\ sqrt {7}} {2}},}

{\ Displaystyle \ sin A \ sin B- \ sin B \ sin C + \ sin C \ sin A = 0,}

{\ Displaystyle \ sin A \ sin B \ sin C = {\ frac {\ sqrt {7}} {8}}.}

Para un número entero $n$ , fijamos $S ( n ) = (-sen A ) n + sen n B + sen n C$ . Entonces tenemos

no	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	dieciséis	17	18	19	20
S ( n )	3	${\ Displaystyle {\ tfrac {\ sqrt {7}} {2}}}$	${\ displaystyle {\ tfrac {7} {2 ^ {2}}}}$	${\ Displaystyle {\ tfrac {\ sqrt {7}} {2}}}$	${\ Displaystyle {\ tfrac {7 \ cdot 3} {2 ^ {4}}}}$	${\ Displaystyle {\ tfrac {7 {\ sqrt {7}}} {2 ^ {4}}}}$	${\ Displaystyle {\ tfrac {7 \ cdot 5} {2 ^ {5}}}}$	${\ Displaystyle {\ tfrac {7 ^ {2} {\ sqrt {7}}} {2 ^ {7}}}}$	${\ Displaystyle {\ tfrac {7 ^ {2} \ cdot 5} {2 ^ {8}}}}$	${\ Displaystyle {\ tfrac {7 \ cdot 25 {\ sqrt {7}}} {2 ^ {9}}}}$	${\ Displaystyle {\ tfrac {7 ^ {2} \ cdot 9} {2 ^ {9}}}}$	${\ Displaystyle {\ tfrac {7 ^ {2} \ cdot 13 {\ sqrt {7}}} {2 ^ {11}}}}$	${\ Displaystyle {\ tfrac {7 ^ {2} \ cdot 33} {2 ^ {11}}}}$	${\ Displaystyle {\ tfrac {7 ^ {2} \ cdot 3 {\ sqrt {7}}} {2 ^ {9}}}}$	${\ Displaystyle {\ tfrac {7 ^ {4} \ cdot 5} {2 ^ {14}}}}$	${\ Displaystyle {\ tfrac {7 ^ {2} \ cdot 179 {\ sqrt {7}}} {2 ^ {15}}}}$	${\ Displaystyle {\ tfrac {7 ^ {3} \ cdot 131} {2 ^ {16}}}}$	${\ Displaystyle {\ tfrac {7 ^ {3} \ cdot 3 {\ sqrt {7}}} {2 ^ {12}}}}$	${\ displaystyle {\ tfrac {7 ^ {3} \ cdot 493} {2 ^ {18}}}}$	${\ Displaystyle {\ tfrac {7 ^ {3} \ cdot 181 {\ sqrt {7}}} {2 ^ {18}}}}$	${\ displaystyle {\ tfrac {7 ^ {5} \ cdot 19} {2 ^ {19}}}}$
S (- n )	3	0	2 3	${\ Displaystyle - {\ tfrac {2 ^ {3} \ cdot 3 {\ sqrt {7}}} {7}}}$	2 5	${\ Displaystyle - {\ tfrac {2 ^ {5} \ cdot 5 {\ sqrt {7}}} {7}}}$	${\ Displaystyle {\ tfrac {2 ^ {6} \ cdot 17} {7}}}$	${\ Displaystyle -2 ^ {7} {\ sqrt {7}}}$	${\ Displaystyle {\ tfrac {2 ^ {9} \ cdot 11} {7}}}$	${\ Displaystyle - {\ tfrac {2 ^ {10} \ cdot 33 {\ sqrt {7}}} {7 ^ {2}}}}$	${\ Displaystyle {\ tfrac {2 ^ {10} \ cdot 29} {7}}}$	${\ Displaystyle - {\ tfrac {2 ^ {14} \ cdot 11 {\ sqrt {7}}} {7 ^ {2}}}}$	${\ displaystyle {\ tfrac {2 ^ {12} \ cdot 269} {7 ^ {2}}}}$	${\ Displaystyle - {\ tfrac {2 ^ {13} \ cdot 117 {\ sqrt {7}}} {7 ^ {2}}}}$	${\ Displaystyle {\ tfrac {2 ^ {14} \ cdot 51} {7}}}$	${\ Displaystyle - {\ tfrac {2 ^ {21} \ cdot 17 {\ sqrt {7}}} {7 ^ {3}}}}$	${\ displaystyle {\ tfrac {2 ^ {17} \ cdot 237} {7 ^ {2}}}}$	${\ Displaystyle - {\ tfrac {2 ^ {17} \ cdot 1445 {\ sqrt {7}}} {7 ^ {3}}}}$	${\ Displaystyle {\ tfrac {2 ^ {19} \ cdot 2203} {7 ^ {3}}}}$	${\ Displaystyle - {\ tfrac {2 ^ {19} \ cdot 1919 {\ sqrt {7}}} {7 ^ {3}}}}$	${\ Displaystyle {\ tfrac {2 ^ {20} \ cdot 5851} {7 ^ {3}}}}$

Con cosenos

Los cosenos en los ángulos $cos A$ , $cos B$ , $cos C$ son las raíces de la ecuación cúbica:

{\ displaystyle x ^ {3} + {\ frac {1} {2}} x ^ {2} - {\ frac {1} {2}} x - {\ frac {1} {8}} = 0. }

Para un número entero $n$ , fijamos $C ( n ) = (cos A ) n + cos n B + cos n C$ . Entonces tenemos

no	0	1	2	3	4	5	6	7	8	9	10
C ( n )	3	$- {\ frac 12}$	${\ Displaystyle {\ frac {5} {4}}}$	$- {\ frac 12}$	${\ Displaystyle {\ frac {13} {16}}}$	$- {\ frac 12}$	${\ Displaystyle {\ frac {19} {32}}}$	${\ Displaystyle - {\ frac {57} {128}}}$	${\ Displaystyle {\ frac {117} {256}}}$	${\ Displaystyle - {\ frac {193} {512}}}$	${\ Displaystyle {\ frac {185} {512}}}$
C (- n )	3	-4	24	-88	416	-1824	8256	-36992	166400	-747520	3359744

Con tangentes

Las tangentes en los ángulos $tan A$ , $tan B$ , $tan C$ son las raíces de la ecuación cúbica:

{\ Displaystyle x ^ {3} + {\ sqrt {7}} x ^ {2} -7x + {\ sqrt {7}} = 0.}

Los cuadrados de las tangentes en los ángulos $tan 2 A$ , $tan 2 B$ , $tan 2 C$ son las raíces de la ecuación cúbica:

{\ Displaystyle x ^ {3} -21x ^ {2} + 35x-7 = 0.}

Para un número entero $n$ , fijamos $T ( n ) = tan n A + tan n B + tan n C$ . Entonces tenemos

no	0	1	2	3	4	5	6	7	8	9	10
T ( n )	3	${\ Displaystyle - {\ sqrt {7}}}$	${\ Displaystyle 7 \ cdot 3}$	${\ Displaystyle -31 {\ sqrt {7}}}$	${\ Displaystyle 7 \ cdot 53}$	${\ Displaystyle -7 \ cdot 87 {\ sqrt {7}}}$	${\ Displaystyle 7 \ cdot 1011}$	${\ Displaystyle -7 ^ {2} \ cdot 239 {\ sqrt {7}}}$	${\ Displaystyle 7 ^ {2} \ cdot 2771}$	${\ Displaystyle -7 \ cdot 32119 {\ sqrt {7}}}$	${\ Displaystyle 7 ^ {2} \ cdot 53189}$
T (- n )	3	${\ sqrt {7}}$	5	${\ Displaystyle {\ frac {25 {\ sqrt {7}}} {7}}}$	19	${\ Displaystyle {\ frac {103 {\ sqrt {7}}} {7}}}$	${\ displaystyle {\ frac {563} {7}}}$	${\ Displaystyle 7 \ cdot 9 {\ sqrt {7}}}$	${\ displaystyle {\ frac {2421} {7}}}$	${\ Displaystyle {\ frac {13297 {\ sqrt {7}}} {7 ^ {2}}}}$	${\ displaystyle {\ frac {10435} {7}}}$

Fórmulas mixtas

También tenemos

{\ Displaystyle \ tan A-4 \ sin B = - {\ sqrt {7}},}

{\ Displaystyle \ tan B-4 \ sin C = - {\ sqrt {7}},}

{\ Displaystyle \ tan C + 4 \ sin A = - {\ sqrt {7}}.}

También tenemos

{\ Displaystyle \ cot ^ {2} A = 1 - {\ frac {2 \ tan C} {\ sqrt {7}}},}

{\ Displaystyle \ cot ^ {2} B = 1 - {\ frac {2 \ tan A} {\ sqrt {7}}},}

{\ Displaystyle \ cot ^ {2} C = 1 - {\ frac {2 \ tan B} {\ sqrt {7}}}.}

{\ Displaystyle \ cos A = - {\ frac {1} {2}} + {\ frac {4} {\ sqrt {7}}} \ sin ^ {3} C,}

{\ Displaystyle \ cos ^ {2} A = {\ frac {3} {4}} + {\ frac {2} {\ sqrt {7}}} \ sin ^ {3} A,}

{\ Displaystyle \ cot A = {\ frac {3} {\ sqrt {7}}} + {\ frac {4} {\ sqrt {7}}} \ cos B,}

{\ Displaystyle \ cot ^ {2} A = 3 + {\ frac {8} {\ sqrt {7}}} \ sin A,}

{\ Displaystyle \ cot A = {\ sqrt {7}} + {\ frac {8} {\ sqrt {7}}} \ sin ^ {2} B,}

{\ Displaystyle \ csc ^ {3} A = - {\ frac {6} {\ sqrt {7}}} + {\ frac {2} {\ sqrt {7}}} \ tan ^ {2} C,}

{\ Displaystyle \ sec A = 2 + 4 \ cos C,}

{\ Displaystyle \ sec A = 6-8 \ sin ^ {2} B,}

{\ Displaystyle \ sec A = 4 - {\ frac {16} {\ sqrt {7}}} \ sin ^ {3} B,}

{\ Displaystyle \ sin ^ {2} A = {\ frac {1} {2}} + {\ frac {1} {2}} \ cos B,}

{\ Displaystyle \ sin ^ {3} A = - {\ frac {\ sqrt {7}} {8}} + {\ frac {\ sqrt {7}} {4}} \ cos B,}

También tenemos

{\ Displaystyle \ sin ^ {3} B \ sin C- \ sin ^ {3} C \ sin A- \ sin ^ {3} A \ sin B = 0,}

{\ Displaystyle \ sin B \ sin ^ {3} C- \ sin C \ sin ^ {3} A- \ sin A \ sin ^ {3} B = {\ frac {7} {2 ^ {4}}} ,}

{\ Displaystyle \ sin ^ {4} B \ sin C- \ sin ^ {4} C \ sin A + \ sin ^ {4} A \ sin B = 0,}

{\ Displaystyle \ sin B \ sin ^ {4} C + \ sin C \ sin ^ {4} A- \ sin A \ sin ^ {4} B = {\ frac {7 {\ sqrt {7}}} { 2 ^ {5}}},}

{\ Displaystyle \ sin ^ {11} B \ sin ^ {3} C- \ sin ^ {11} C \ sin ^ {3} A- \ sin ^ {11} A \ sin ^ {3} B = 0, }

{\ Displaystyle \ sin ^ {3} B \ sin ^ {11} C- \ sin ^ {3} C \ sin ^ {11} A- \ sin ^ {3} A \ sin ^ {11} B = {\ frac {7 ^ {3} \ cdot 17} {2 ^ {14}}}.}

Identidades de tipo Ramanujan

También se pueden obtener identidades similares a las descubiertas por Srinivasa Ramanujan

{\ Displaystyle {\ sqrt [{3}] {2 \ sin \ left ({\ frac {2 \ pi} {7}} \ right)}} + {\ sqrt [{3}] {2 \ sin \ left ({\ frac {4 \ pi} {7}} \ right)}} + {\ sqrt [{3}] {2 \ sin \ left ({\ frac {8 \ pi} {7}} \ right)} } = \ left (- {\ sqrt [{18}] {7}} \ right) {\ sqrt [{3}] {- {\ sqrt [{3}] {7}} + 6 + 3 \ left ( {\ sqrt [{3}] {5-3 {\ sqrt [{3}] {7}}}} + {\ sqrt [{3}] {4-3 {\ sqrt [{3}] {7} }}} \ derecho)}}}

{\ Displaystyle {\ frac {1} {\ sqrt [{3}] {2 \ sin \ left ({\ frac {2 \ pi} {7}} \ right)}}} + {\ frac {1} { \ sqrt [{3}] {2 \ sin \ left ({\ frac {4 \ pi} {7}} \ right)}}} + {\ frac {1} {\ sqrt [{3}] {2 \ sin \ left ({\ frac {8 \ pi} {7}} \ right)}}} = \ left (- {\ frac {1} {\ sqrt [{18}] {7}}} \ right) { \ sqrt [{3}] {6 + 3 \ left ({\ sqrt [{3}] {5-3 {\ sqrt [{3}] {7}}}} + {\ sqrt [{3}] { 4-3 {\ sqrt [{3}] {7}}}} \ right)}}}

{\ Displaystyle {\ sqrt [{3}] {4 \ sin ^ {2} \ left ({\ frac {2 \ pi} {7}} \ right)}} + {\ sqrt [{3}] {4 \ sin ^ {2} \ left ({\ frac {4 \ pi} {7}} \ right)}} + {\ sqrt [{3}] {4 \ sin ^ {2} \ left ({\ frac { 8 \ pi} {7}} \ right)}} = \ left ({\ sqrt [{18}] {49}} \ right) {\ sqrt [{3}] {{\ sqrt [{3}] { 49}} + 6 + 3 \ left ({\ sqrt [{3}] {12 + 3 ({\ sqrt [{3}] {49}} + 2 {\ sqrt [{3}] {7}}) }} + {\ sqrt [{3}] {11 + 3 ({\ sqrt [{3}] {49}} + 2 {\ sqrt [{3}] {7}})}} \ right)}} }

{\ Displaystyle {\ frac {1} {\ sqrt [{3}] {4 \ sin ^ {2} \ left ({\ frac {2 \ pi} {7}} \ right)}}} + {\ frac {1} {\ sqrt [{3}] {4 \ sin ^ {2} \ left ({\ frac {4 \ pi} {7}} \ right)}}} + {\ frac {1} {\ sqrt [{3}] {4 \ sin ^ {2} \ left ({\ frac {8 \ pi} {7}} \ right)}}} = \ left ({\ frac {1} {\ sqrt [{18 }] {49}}} \ right) {\ sqrt [{3}] {2 {\ sqrt [{3}] {7}} + 6 + 3 \ left ({\ sqrt [{3}] {12+ 3 ({\ sqrt [{3}] {49}} + 2 {\ sqrt [{3}] {7}})}} + {\ sqrt [{3}] {11 + 3 ({\ sqrt [{ 3}] {49}} + 2 {\ sqrt [{3}] {7}})}} \ right)}}}

{\ Displaystyle {\ sqrt [{3}] {2 \ cos \ left ({\ frac {2 \ pi} {7}} \ right)}} + {\ sqrt [{3}] {2 \ cos \ left ({\ frac {4 \ pi} {7}} \ right)}} + {\ sqrt [{3}] {2 \ cos \ left ({\ frac {8 \ pi} {7}} \ right)} } = {\ sqrt [{3}] {5-3 {\ sqrt [{3}] {7}}}}}

{\ Displaystyle {\ frac {1} {\ sqrt [{3}] {2 \ cos \ left ({\ frac {2 \ pi} {7}} \ right)}}} + {\ frac {1} { \ sqrt [{3}] {2 \ cos \ left ({\ frac {4 \ pi} {7}} \ right)}}} + {\ frac {1} {\ sqrt [{3}] {2 \ cos \ left ({\ frac {8 \ pi} {7}} \ right)}}} = {\ sqrt [{3}] {4-3 {\ sqrt [{3}] {7}}}}}

{\ Displaystyle {\ sqrt [{3}] {4 \ cos ^ {2} \ left ({\ frac {2 \ pi} {7}} \ right)}} + {\ sqrt [{3}] {4 \ cos ^ {2} \ left ({\ frac {4 \ pi} {7}} \ right)}} + {\ sqrt [{3}] {4 \ cos ^ {2} \ left ({\ frac { 8 \ pi} {7}} \ right)}} = {\ sqrt [{3}] {11 + 3 (2 {\ sqrt [{3}] {7}} + {\ sqrt [{3}] { 49}})}}}

{\ Displaystyle {\ frac {1} {\ sqrt [{3}] {4 \ cos ^ {2} \ left ({\ frac {2 \ pi} {7}} \ right)}}} + {\ frac {1} {\ sqrt [{3}] {4 \ cos ^ {2} \ left ({\ frac {4 \ pi} {7}} \ right)}}} + {\ frac {1} {\ sqrt [{3}] {4 \ cos ^ {2} \ left ({\ frac {8 \ pi} {7}} \ right)}}} = {\ sqrt [{3}] {12 + 3 (2 { \ sqrt [{3}] {7}} + {\ sqrt [{3}] {49}})}}}

{\ Displaystyle {\ sqrt [{3}] {\ tan \ left ({\ frac {2 \ pi} {7}} \ right)}} + {\ sqrt [{3}] {\ tan \ left ({ \ frac {4 \ pi} {7}} \ right)}} + {\ sqrt [{3}] {\ tan \ left ({\ frac {8 \ pi} {7}} \ right)}} = \ izquierda (- {\ sqrt [{18}] {7}} \ right) {\ sqrt [{3}] {{\ sqrt [{3}] {7}} + 6 + 3 \ left ({\ sqrt [ {3}] {5 + 3 ({\ sqrt [{3}] {7}} - {\ sqrt [{3}] {49}})}} + {\ sqrt [{3}] {- 3+ 3 ({\ sqrt [{3}] {7}} - {\ sqrt [{3}] {49}})}} \ right)}}}

{\ Displaystyle {\ frac {1} {\ sqrt [{3}] {\ tan \ left ({\ frac {2 \ pi} {7}} \ right)}}} + {\ frac {1} {\ sqrt [{3}] {\ tan \ left ({\ frac {4 \ pi} {7}} \ right)}}} + {\ frac {1} {\ sqrt [{3}] {\ tan \ left ({\ frac {8 \ pi} {7}} \ right)}}} = \ left (- {\ frac {1} {\ sqrt [{18}] {7}}} \ right) {\ sqrt [ {3}] {- {\ sqrt [{3}] {49}} + 6 + 3 \ left ({\ sqrt [{3}] {5 + 3 ({\ sqrt [{3}] {7}} - {\ sqrt [{3}] {49}})}} + {\ sqrt [{3}] {- 3 + 3 ({\ sqrt [{3}] {7}} - {\ sqrt [{3 }] {49}})}} \ right)}}}

{\ Displaystyle {\ sqrt [{3}] {\ tan ^ {2} \ left ({\ frac {2 \ pi} {7}} \ right)}} + {\ sqrt [{3}] {\ tan ^ {2} \ left ({\ frac {4 \ pi} {7}} \ right)}} + {\ sqrt [{3}] {\ tan ^ {2} \ left ({\ frac {8 \ pi } {7}} \ right)}} = \ left ({\ sqrt [{18}] {49}} \ right) {\ sqrt [{3}] {3 {\ sqrt [{3}] {49} } + 6 + 3 \ left ({\ sqrt [{3}] {89 + 3 (3 {\ sqrt [{3}] {49}} + 5 {\ sqrt [{3}] {7}})} } + {\ sqrt [{3}] {25 + 3 (3 {\ sqrt [{3}] {49}} + 5 {\ sqrt [{3}] {7}})}} \ right)}} }

{\ Displaystyle {\ frac {1} {\ sqrt [{3}] {\ tan ^ {2} \ left ({\ frac {2 \ pi} {7}} \ right)}}} + {\ frac { 1} {\ sqrt [{3}] {\ tan ^ {2} \ left ({\ frac {4 \ pi} {7}} \ right)}}} + {\ frac {1} {\ sqrt [{ 3}] {\ tan ^ {2} \ left ({\ frac {8 \ pi} {7}} \ right)}}} = \ left ({\ frac {1} {\ sqrt [{18}] { 49}}} \ right) {\ sqrt [{3}] {5 {\ sqrt [{3}] {7}} + 6 + 3 \ left ({\ sqrt [{3}] {89 + 3 (3 {\ sqrt [{3}] {49}} + 5 {\ sqrt [{3}] {7}})}} + {\ sqrt [{3}] {25 + 3 (3 {\ sqrt [{3 }] {49}} + 5 {\ sqrt [{3}] {7}})}} \ right)}}}

También tenemos

{\ Displaystyle {\ sqrt [{3}] {\ cos \ left ({\ frac {2 \ pi} {7}} \ right) / \ cos \ left ({\ frac {4 \ pi} {7}} \ right)}} + {\ sqrt [{3}] {\ cos \ left ({\ frac {4 \ pi} {7}} \ right) / \ cos \ left ({\ frac {8 \ pi} { 7}} \ right)}} + {\ sqrt [{3}] {\ cos \ left ({\ frac {8 \ pi} {7}} \ right) / \ cos \ left ({\ frac {2 \ pi} {7}} \ right)}} = - {\ sqrt [{3}] {7}}.}

{\ Displaystyle {\ sqrt [{3}] {\ cos \ left ({\ frac {4 \ pi} {7}} \ right) / \ cos \ left ({\ frac {2 \ pi} {7}} \ right)}} + {\ sqrt [{3}] {\ cos \ left ({\ frac {8 \ pi} {7}} \ right) / \ cos \ left ({\ frac {4 \ pi} { 7}} \ right)}} + {\ sqrt [{3}] {\ cos \ left ({\ frac {2 \ pi} {7}} \ right) / \ cos \ left ({\ frac {8 \ pi} {7}} \ right)}} = 0.}

{\ Displaystyle {\ sqrt [{3}] {2 \ sin \ left ({\ frac {2 \ pi} {7}} \ right)}} + {\ sqrt [{3}] {2 \ sin \ left ({\ frac {4 \ pi} {7}} \ right)}} + {\ sqrt [{3}] {2 \ sin \ left ({\ frac {8 \ pi} {7}} \ right)} } = \ left (- {\ sqrt [{18}] {7}} \ right) {\ sqrt [{3}] {- {\ sqrt [{3}] {7}} + 6 + 3 \ left ( {\ sqrt [{3}] {5-3 {\ sqrt [{3}] {7}}}} + {\ sqrt [{3}] {4-3 {\ sqrt [{3}] {7} }}} \ derecho)}}}

{\ Displaystyle {\ sqrt [{3}] {\ cos ^ {4} \ left ({\ frac {4 \ pi} {7}} \ right) / \ cos \ left ({\ frac {2 \ pi} {7}} \ right)}} + {\ sqrt [{3}] {\ cos ^ {4} \ left ({\ frac {8 \ pi} {7}} \ right) / \ cos \ left ({ \ frac {4 \ pi} {7}} \ right)}} + {\ sqrt [{3}] {\ cos ^ {4} \ left ({\ frac {2 \ pi} {7}} \ right) / \ cos \ left ({\ frac {8 \ pi} {7}} \ right)}} = - {\ sqrt [{3}] {49}} / 2.}

{\ Displaystyle {\ sqrt [{3}] {\ cos ^ {5} \ left ({\ frac {2 \ pi} {7}} \ right) / \ cos ^ {2} \ left ({\ frac { 4 \ pi} {7}} \ right)}} + {\ sqrt [{3}] {\ cos ^ {5} \ left ({\ frac {4 \ pi} {7}} \ right) / \ cos ^ {2} \ left ({\ frac {8 \ pi} {7}} \ right)}} + {\ sqrt [{3}] {\ cos ^ {5} \ left ({\ frac {8 \ pi } {7}} \ right) / \ cos ^ {2} \ left ({\ frac {2 \ pi} {7}} \ right)}} = 0.}

{\ Displaystyle {\ sqrt [{3}] {\ cos ^ {5} \ left ({\ frac {4 \ pi} {7}} \ right) / \ cos ^ {2} \ left ({\ frac { 2 \ pi} {7}} \ right)}} + {\ sqrt [{3}] {\ cos ^ {5} \ left ({\ frac {8 \ pi} {7}} \ right) / \ cos ^ {2} \ left ({\ frac {4 \ pi} {7}} \ right)}} + {\ sqrt [{3}] {\ cos ^ {5} \ left ({\ frac {2 \ pi } {7}} \ right) / \ cos ^ {2} \ left ({\ frac {8 \ pi} {7}} \ right)}} = - 3 {\ sqrt [{3}] {7}} / 2.}

{\ Displaystyle {\ sqrt [{3}] {\ cos ^ {14} \ left ({\ frac {2 \ pi} {7}} \ right) / \ cos ^ {5} \ left ({\ frac { 4 \ pi} {7}} \ right)}} + {\ sqrt [{3}] {\ cos ^ {14} \ left ({\ frac {4 \ pi} {7}} \ right) / \ cos ^ {5} \ left ({\ frac {8 \ pi} {7}} \ right)}} + {\ sqrt [{3}] {\ cos ^ {14} \ left ({\ frac {8 \ pi } {7}} \ right) / \ cos ^ {5} \ left ({\ frac {2 \ pi} {7}} \ right)}} = 0.}

{\ Displaystyle {\ sqrt [{3}] {\ cos ^ {14} \ left ({\ frac {4 \ pi} {7}} \ right) / \ cos ^ {5} \ left ({\ frac { 2 \ pi} {7}} \ right)}} + {\ sqrt [{3}] {\ cos ^ {14} \ left ({\ frac {8 \ pi} {7}} \ right) / \ cos ^ {5} \ left ({\ frac {4 \ pi} {7}} \ right)}} + {\ sqrt [{3}] {\ cos ^ {14} \ left ({\ frac {2 \ pi } {7}} \ right) / \ cos ^ {5} \ left ({\ frac {8 \ pi} {7}} \ right)}} = - 61 {\ sqrt [{3}] {7}} / 8.}

Notas y referencias

(fr) Este artículo está tomado parcial o totalmente del artículo de Wikipedia en inglés titulado " Triángulo heptagonal " ( ver la lista de autores ) .

(en) Paul Yiu, “ heptagonal Triángulos y sus acompañantes ” , Foro Geometricorum , vol. 9,2009, p. 125–148 ( leer en línea ).
(en) Leon Bankoff y Jack Garfunkel, " El triángulo heptagonal " , Revista de matemáticas , n o 46 (1),Enero de 1973, p. 7-19 ( DOI https://doi.org/10.1080/0025570X.1973.11976267 , leer en línea ).
(en) Abdilkadir Altintas, “ Algunos colinealidades en el heptagonal Triángulo ” , Foro Geometricorum , vol. dieciséis,2016, p. 249-256 ( leer en línea ).
(en) Kai Wang, “ Triángulo heptagonal e identidades trigonométricas ” , Forum Geometricorum , vol. 19,2019, p. 29–38 ( leer en línea ).
(in) Kai Wang, " Tenemos ecuaciones cúbicas con cero sumas de raíces cúbicas de raíces " .
(es) Eric W. Weisstein , “ heptagonal Triángulo, ” en MathWorld .
(en) Kai Wang, " Propiedades trigonométricas para un triángulo heptagonal " .
(en) Andrew Mattei Gleason , " Trisección de ángulo, el heptágono y el triskaidecágono " , American Mathematical Monthly , vol. 95, n o 3,Marzo de 1988, p. 185-194 ( DOI 10.2307 / 2323624 , leer en línea [ archivo de19 de diciembre de 2015] ).
(en) Victor Hugo Moll (de) , Una ecuación trigonométrica elemental , https://arxiv.org/abs/0709.3755 2007.
(en) Wang, Kai. [1] .
(en) Roman Wituła y Damian Słota, " Nuevas fórmulas de tipo Ramanujan y números de cuasi Fibonacci de orden 7 " , Journal of Integer Sequences , vol. 10,2007.