Cuadrupolo

En electrocinética , un cuadrupolo (o cuadrupolo ) es un elemento modelo de un circuito eléctrico en el que se considera como un bloque con dos conexiones de entrada y dos de salida. Estudiamos la transferencia de magnitudes eléctricas, voltaje y corriente , entre estos dos dipolos caracterizados por una impedancia , en función del tiempo.

Cuando el estudio del cuadrupolo se refiere a una señal eléctrica , la magnitud de entrada y salida puede ser diferente ( voltaje , corriente ). La posible contribución de energía al circuito, que luego se dice que está activo , no forma parte del modelo. Los primeros estudios sobre cuadripolos los debemos al matemático alemán Franz Breisig , en la década de 1920 .

La analogía electromecánica permite el uso del formalismo cuadrupolo para transductores o sistemas mecánicos o electromecánicos.

General

Definiciones

Un cuadrupolo es un componente o circuito electrónico que se ve como una caja negra con dos puertos eléctricos. Nos interesa la corriente y el voltaje en cada uno de los puertos, con las convenciones que se muestran a continuación: las corrientes que ingresan al cuadrupolo en el polo positivo del voltaje se anotan positivamente .

Tamaño físico	Entrada	Salida
Actual	I1{\ Displaystyle I_ {1}} o Imi{\ Displaystyle I_ {e}}	I2{\ Displaystyle I_ {2}} o Is{\ Displaystyle I_ {s}}
Voltaje	V1{\ Displaystyle V_ {1}} o Umi{\ Displaystyle U_ {e}}	V2{\ Displaystyle V_ {2}} o Us{\ Displaystyle U_ {s}}

Esta convención equilibra la entrada y la salida. El cuadripolo está determinado por dos ecuaciones características que permiten, conociendo los de los dispositivos conectados a él, calcular los valores de entrada y salida.

Función de transferencia

La función de transferencia de un cuadrupolo lineal en régimen de alternancia sinusoidal tiene las siguientes propiedades: T_{\ Displaystyle {\ underline {T}}}

- Es un número complejo . Este número depende de la frecuencia y la carga colocada en la salida. T_=T_(jω){\ Displaystyle {\ underline {T}} = {\ underline {T}} (j \ omega)}

- , a veces simplemente indicado , es la relación entre los valores rms de la señal de salida y la señal de entrada. |T_|{\ Displaystyle | {\ underline {T}} |}T{\ Displaystyle T}

- es la diferencia de fase (o desplazamiento de fase) de la señal de salida con respecto a la señal de entrada. arg⁡(T_){\ Displaystyle \ arg {({\ underline {T}})}}

Coeficientes de amplificación

Los coeficientes de amplificación son funciones de transferencia especiales.

• Coeficiente de amplificación de voltaje: T=Av=UsUmi{\ Displaystyle T = A_ {v} = {\ frac {U_ {s}} {U_ {e}}}}
• Coeficiente de amplificación actual: T=AI=IsImi{\ Displaystyle T = A_ {i} = {\ frac {I_ {s}} {I_ {e}}}}

• coeficiente de amplificación de potencia, aunque no es una proporción de números complejos asociados con señales:

Apag=UsIsporque⁡(φs)UmiImiporque⁡(φmi){\ Displaystyle A_ {p} = {\ frac {U_ {s} I_ {s} \ cos {(\ varphi _ {s})}} {U_ {e} I_ {e} \ cos {(\ varphi _ { mi})}}}}con (respectivamente ) el desplazamiento de fase de con respecto a (respectivamente de con respecto a ). φs{\ Displaystyle \ varphi _ {s}}φmi{\ Displaystyle \ varphi _ {e}}Us{\ Displaystyle U_ {s}}Is{\ Displaystyle I_ {s}}Umi{\ Displaystyle U_ {e}}Imi{\ Displaystyle I_ {e}}

Estos coeficientes generalmente dependen de la frecuencia y la carga de salida.

Ganancias

Como los módulos de estos coeficientes pueden variar considerablemente cuando varía la frecuencia, se utiliza otra cantidad que "aprieta" estas variaciones.

• Ganancia de voltaje: GRAMOV=20Iniciar sesión⁡(USUmi){\ Displaystyle G_ {V} = 20 \ log \ left ({\ frac {U_ {S}} {U_ {E}}} \ right)}

• Ganancia de corriente: GRAMOI=20Iniciar sesión⁡(ISImi){\ Displaystyle G_ {I} = 20 \ log \ left ({\ frac {I_ {S}} {I_ {E}}} \ right)}
• Ganancia de potencia: GRAMOPAG=10Iniciar sesión⁡(PAGSPAGmi){\ Displaystyle G_ {P} = 10 \ log \ left ({\ frac {P_ {S}} {P_ {E}}} \ right)}

Las ganancias se expresan en decibelios .

• Cuando T se multiplica por 10, G = 20logT aumenta en 20  dB  ;
• La ganancia se vuelve negativa si T <1.
• Cuando Av se duplica, Gv aumenta en 6  dB .

Parametrización de un cuadrupolo lineal

Los cuadripolos se representan en forma de matrices que conectan las corrientes y los voltajes, cuyos términos pueden depender de la frecuencia. Podemos construir estas matrices de diferentes formas: todas son equivalentes, pero la construcción más práctica dependerá de los problemas a resolver.

Configuración de transferencia o cascada

Expresamos los datos de la izquierda en función de los de la derecha. Los términos se indican como ABCD o , de acuerdo con las convenciones: TIj{\ Displaystyle T_ {ij}}aIj{\ Displaystyle a_ {ij}}(V1I1)=(ABVSD)(V2-I2){\ displaystyle {V_ {1} \ choose I_ {1}} = {\ begin {pmatrix} A&B \\ C&D \ end {pmatrix}} {V_ {2} \ choose -I_ {2}}},

O a la inversa, escribimos los términos de la derecha de acuerdo con los términos de la izquierda. Es la A'B'C'D matriz', o , inversa de la anterior: TIj′{\ Displaystyle T '_ {ij}}BIj{\ Displaystyle b_ {ij}}

(V2-I2)=(A′B′VS′D′)(V1I1){\ Displaystyle {V_ {2} \ choose -I_ {2}} = {\ begin {pmatrix} A '& B' \\ C '& D' \ end {pmatrix}} {V_ {1} \ choose I_ { 1}}},

A y D son adimensionales , B está en ohmios y C en siemens. Este ajuste es adecuado para el encadenamiento de cuadrupolos. La corriente de salida del primer cuadripolo es opuesta a la corriente de entrada del siguiente cuadripolo, de ahí el signo "-".

Ajuste de impedancia

Expresamos los voltajes en función de las corrientes:(V1V2)=(Z11Z12Z21Z22)(I1I2){\ Displaystyle {V_ {1} \ choose V_ {2}} = {\ begin {pmatrix} Z_ {11} & Z_ {12} \\ Z_ {21} & Z_ {22} \ end {pmatrix}} {I_ {1} \ elija I_ {2}}},con :Z11=V1I1|I2=0Z12=V1I2|I1=0{\ Displaystyle Z_ {11} = {V_ {1} \ over I_ {1}} {\ bigg |} _ {I_ {2} = 0} \ qquad Z_ {12} = {V_ {1} \ over I_ { 2}} {\ bigg |} _ {I_ {1} = 0}} yZ21=V2I1|I2=0Z22=V2I2|I1=0{\ Displaystyle Z_ {21} = {V_ {2} \ over I_ {1}} {\ bigg |} _ {I_ {2} = 0} \ qquad Z_ {22} = {V_ {2} \ over I_ { 2}} {\ bigg |} _ {I_ {1} = 0}}

La impedancia de entrada del cuadrupolo se llama; la impedancia de transferencia inversa del cuadrupolo; la impedancia de transferencia del cuadrupolo; la impedancia de salida del cuadrupolo. Todos estos términos están en ohmios. Z11{\ Displaystyle Z_ {11}}Z12{\ Displaystyle Z_ {12}}Z21{\ Displaystyle Z_ {21}}Z22{\ Displaystyle Z_ {22}}

Ajuste de parámetros en admitancias

Las corrientes se expresan en función de las tensiones: (I1I2)=(Y11Y12Y21Y22)(V1V2){\ Displaystyle {I_ {1} \ choose I_ {2}} = {\ begin {pmatrix} Y_ {11} & Y_ {12} \\ Y_ {21} & Y_ {22} \ end {pmatrix}} {V_ {1} \ elija V_ {2}}},con :Y11=I1V1|V2=0Y12=I1V2|V1=0{\ Displaystyle Y_ {11} = {I_ {1} \ over V_ {1}} {\ bigg |} _ {V_ {2} = 0} \ qquad Y_ {12} = {I_ {1} \ over V_ { 2}} {\ bigg |} _ {V_ {1} = 0}} yY21=I2V1|V2=0Y22=I2V2|V1=0{\ Displaystyle Y_ {21} = {I_ {2} \ over V_ {1}} {\ bigg |} _ {V_ {2} = 0} \ qquad Y_ {22} = {I_ {2} \ over V_ { 2}} {\ bigg |} _ {V_ {1} = 0}}

La admitancia de entrada del cuadrupolo se llama; la admitancia de transferencia inversa del cuadrupolo; la admitancia de transferencia del cuadrupolo; la admitancia de salida cuadrupolo. Todos los términos son admitancias, por lo tanto expresados ​​en siemens. Y11{\ Displaystyle Y_ {11}}Y12{\ Displaystyle Y_ {12}}Y21{\ Displaystyle Y_ {21}}Y22{\ Displaystyle Y_ {22}}

Configuración híbrida

Estas relaciones son útiles al estudiar transistores. (ver # Quadripôles_passifs )

(V1I2)=(H11H12H21H22)(I1V2){\ Displaystyle {V_ {1} \ choose I_ {2}} = {\ begin {pmatrix} H_ {11} & H_ {12} \\ H_ {21} & H_ {22} \ end {pmatrix}} {I_ {1} \ elija V_ {2}}} , con : H11=V1I1|V2=0H12=V1V2|I1=0{\ Displaystyle H_ {11} = {V_ {1} \ over I_ {1}} {\ bigg |} _ {V_ {2} = 0} \ qquad H_ {12} = {V_ {1} \ over V_ { 2}} {\ bigg |} _ {I_ {1} = 0}} y H21=I2I1|V2=0H22=I2V2|I1=0{\ Displaystyle H_ {21} = {I_ {2} \ over I_ {1}} {\ bigg |} _ {V_ {2} = 0} \ qquad H_ {22} = {I_ {2} \ over V_ { 2}} {\ bigg |} _ {I_ {1} = 0}}

Se puede notar eso y aquello . H11=1/Y11{\ Displaystyle H_ {11} = 1 / Y_ {11}}H22=1/Z22{\ Displaystyle H_ {22} = 1 / Z_ {22}}

La impedancia de entrada del cuadrupolo (ohmios) se llama; la ganancia de voltaje inverso del cuadrupolo (adimensional); la ganancia de corriente de transferencia del cuadrupolo (adimensional), la admitancia de salida del cuadrupolo (siemens). H11{\ Displaystyle H_ {11}}H12{\ Displaystyle H_ {12}}H21{\ Displaystyle H_ {21}}H22{\ Displaystyle H_ {22}}

La computación matricial se adapta muy bien a los cuadripolos y permite obtener las funciones de transferencia de los circuitos electrónicos cuando otros métodos se pierden en un formalismo abstruso, fuente de errores y pérdida de tiempo.

Configuración híbrida inversa

Las relaciones híbridas inversas se utilizan muy poco, pero existen.

(I1V2)=(GRAMO11GRAMO12GRAMO21GRAMO22)(V1I2){\ displaystyle {I_ {1} \ choose V_ {2}} = {\ begin {pmatrix} G_ {11} & G_ {12} \\ G_ {21} & G_ {22} \ end {pmatrix}} {V_ {1} \ elija I_ {2}}}, con : GRAMO11=I1V1|I2=0GRAMO12=I1I2|V1=0{\ Displaystyle G_ {11} = {I_ {1} \ over V_ {1}} {\ bigg |} _ {I_ {2} = 0} \ qquad G_ {12} = {I_ {1} \ over I_ { 2}} {\ bigg |} _ {V_ {1} = 0}} y GRAMO21=V2V1|I2=0GRAMO22=V2I2|V1=0{\ Displaystyle G_ {21} = {V_ {2} \ over V_ {1}} {\ bigg |} _ {I_ {2} = 0} \ qquad G_ {22} = {V_ {2} \ over I_ { 2}} {\ bigg |} _ {V_ {1} = 0}}

Conversión de matrices

Las configuraciones que se proporcionan a continuación son equivalentes: las conversiones le permiten cambiar de una a otra. Sin embargo, algunos cuadripolos no se pueden describir en determinadas configuraciones, por ejemplo, si las fórmulas de conversión implican una división por cero . representa el determinante de la matriz . Δ{\ Displaystyle \ Delta}

	Configuración de ABCD	Parámetros Z	Parámetros Y	Parámetros H
Matriz de transferencia ABCD	[ABVSD]{\ displaystyle {\ begin {bmatrix} A&B \\ C&D \ end {bmatrix}}}	[Z11Z21ΔZZ211Z21Z22Z21]{\displaystyle {\begin{bmatrix}{\frac {Z_{11}}{Z_{21}}}&{\frac {\Delta Z}{Z_{21}}}\\{\frac {1}{Z_{21}}}&{\frac {Z_{22}}{Z_{21}}}\end{bmatrix}}}	[−Y22Y21−1Y21−ΔYY21−Y11Y21]{\displaystyle {\begin{bmatrix}-{\frac {Y_{22}}{Y_{21}}}&-{\frac {1}{Y_{21}}}\\-{\frac {\Delta Y}{Y_{21}}}&-{\frac {Y_{11}}{Y_{21}}}\end{bmatrix}}}	[−ΔHH21−H11H21−H22H21−1H21]{\displaystyle {\begin{bmatrix}-{\frac {\Delta H}{H_{21}}}&-{\frac {H_{11}}{H_{21}}}\\-{\frac {H_{22}}{H_{21}}}&-{\frac {1}{H_{21}}}\end{bmatrix}}}
Matriz de impedancia Z	[ACΔ(ABCD)C1CDC]{\displaystyle {\begin{bmatrix}{\frac {A}{C}}&{\frac {\Delta (ABCD)}{C}}\\{\frac {1}{C}}&{\frac {D}{C}}\end{bmatrix}}}	[Z11Z12Z21Z22]{\ displaystyle {\ begin {bmatrix} Z_ {11} & Z_ {12} \\ Z_ {21} & Z_ {22} \ end {bmatrix}}}	[Y22ΔY−Y12ΔY−Y21ΔYY11ΔY]{\displaystyle {\begin{bmatrix}{\frac {Y_{22}}{\Delta Y}}&-{\frac {Y_{12}}{\Delta Y}}\\-{\frac {Y_{21}}{\Delta Y}}&{\frac {Y_{11}}{\Delta Y}}\end{bmatrix}}}	[ΔHH22H12H22−H21H221H22]{\displaystyle {\begin{bmatrix}{\frac {\Delta H}{H_{22}}}&{\frac {H_{12}}{H_{22}}}\\-{\frac {H_{21}}{H_{22}}}&{\frac {1}{H_{22}}}\end{bmatrix}}}
Matriz de admisión Y	[DB−Δ(ABCD)B−1BAB]{\displaystyle {\begin{bmatrix}{\frac {D}{B}}&-{\frac {\Delta (ABCD)}{B}}\\-{\frac {1}{B}}&{\frac {A}{B}}\end{bmatrix}}}	[Z22ΔZ−Z12ΔZ−Z21ΔZZ11ΔZ]{\displaystyle {\begin{bmatrix}{\frac {Z_{22}}{\Delta Z}}&-{\frac {Z_{12}}{\Delta Z}}\\-{\frac {Z_{21}}{\Delta Z}}&{\frac {Z_{11}}{\Delta Z}}\end{bmatrix}}}	[Y11Y12Y21Y22]{\ displaystyle {\ begin {bmatrix} Y_ {11} & Y_ {12} \\ Y_ {21} & Y_ {22} \ end {bmatrix}}}	[1H11−H12H11H21H11ΔHH11]{\displaystyle {\begin{bmatrix}{\frac {1}{H_{11}}}&-{\frac {H_{12}}{H_{11}}}\\{\frac {H_{21}}{H_{11}}}&{\frac {\Delta H}{H_{11}}}\end{bmatrix}}}
Matriz híbrida H	[BDΔ(ABCD)D−1DCD]{\displaystyle {\begin{bmatrix}{\frac {B}{D}}&{\frac {\Delta (ABCD)}{D}}\\-{\frac {1}{D}}&{\frac {C}{D}}\end{bmatrix}}}	[ΔZZ22Z12Z22−Z21Z221Z22]{\displaystyle {\begin{bmatrix}{\frac {\Delta Z}{Z_{22}}}&{\frac {Z_{12}}{Z_{22}}}\\-{\frac {Z_{21}}{Z_{22}}}&{\frac {1}{Z_{22}}}\end{bmatrix}}}	[1Y11−Y12Y11Y21Y11ΔYY11]{\displaystyle {\begin{bmatrix}{\frac {1}{Y_{11}}}&-{\frac {Y_{12}}{Y_{11}}}\\{\frac {Y_{21}}{Y_{11}}}&{\frac {\Delta Y}{Y_{11}}}\end{bmatrix}}}	[H11H12H21H22]{\ displaystyle {\ begin {bmatrix} H_ {11} & H_ {12} \\ H_ {21} & H_ {22} \ end {bmatrix}}}

Parámetros S

Los parámetros S (para dispersión , difusión ) están escritos en un enfoque diferente. Aquí consideramos, como se ilustra, el cuadrupolo colocado entre dos líneas de transmisión de impedancia característica . Los parámetros S no relacionan directamente las corrientes y tensiones medidas en los puertos. Están escritos en términos de ondas incidentes y reflejadas, dependen no solo de las características del cuadrupolo, sino también de la línea de transmisión. Z0{\ Displaystyle Z_ {0}}

(B1B2)=(S11S12S21S22)(a1a2){\ Displaystyle {b_ {1} \ choose b_ {2}} = {\ begin {pmatrix} S_ {11} & S_ {12} \\ S_ {21} & S_ {22} \ end {pmatrix}} {a_ {1} \ elija a_ {2}}}

La tensión y la corriente observadas en cada puerto se descomponen en función de las ondas incidente y reflejada, lo que permite relacionar los parámetros S con los parámetros cuadripolo habituales. Como ejemplo, aquí está su escritura a partir de parámetros ABCD:

S11=AZ02+B-VSZ01Z02∗-DZ01∗α{\ Displaystyle S_ {11} = {\ frac {AZ_ {02} + B-CZ_ {01} Z_ {02} ^ {*} - DZ_ {01} ^ {*}} {\ alpha}}}, S12=2(AD-BVS)ℜ(Z01)ℜ(Z02)α{\ Displaystyle S_ {12} = {\ frac {2 (AD-BC) {\ sqrt {\ Re (Z_ {01}) \ Re (Z_ {02})}}} {\ alpha}}}, S21=2ℜ(Z01)ℜ(Z02)α{\ Displaystyle S_ {21} = {\ frac {2 {\ sqrt {\ Re (Z_ {01}) \ Re (Z_ {02})}}} {\ alpha}}}, S22=AZ02∗+B-VSZ01∗Z02-DZ01α{\ Displaystyle S_ {22} = {\ frac {AZ_ {02} ^ {*} + B-CZ_ {01} ^ {*} Z_ {02} -DZ_ {01}} {\ alpha}}}, con α=AZ02+B+VSZ01Z02+DZ01{\ Displaystyle \ alpha = AZ_ {02} + B + CZ_ {01} Z_ {02} + DZ_ {01}}

Esta escritura es genérica: establece que las impedancias de línea pueden ser diferentes a la izquierda y a la derecha ( y respectivamente) y son complejas. En la práctica, hay muchas situaciones en las que las dos impedancias de línea son iguales y reales, lo que simplifica considerablemente la escritura. Z01{\ Displaystyle Z_ {01}}Z02{\ Displaystyle Z_ {02}}

S11=AZ0+B-VSZ02-DZ0α{\ Displaystyle S_ {11} = {\ frac {AZ_ {0} + B-CZ_ {0} ^ {2} -DZ_ {0}} {\ alpha}}}, S12=2(AD-BVS)Z0α{\ Displaystyle S_ {12} = {\ frac {2 (AD-BC) Z_ {0}} {\ alpha}}}, S21=2Z0α{\ displaystyle S_ {21} = {\ frac {2 {Z_ {0}}} {\ alpha}}}, S22=AZ0+B-VSZ02-DZ0α{\ displaystyle S_ {22} = {\ frac {AZ_ {0} + B-CZ_ {0} ^ {2} -DZ_ {0}} {\ alpha}}}, con α=AZ0+B+VSZ02+DZ0{\ Displaystyle \ alpha = AZ_ {0} + B + CZ_ {0} ^ {2} + DZ_ {0}}

Los parámetros S son particularmente interesantes para la caracterización experimental de circuitos de alta frecuencia: se pueden medir directamente con un analizador de redes .

Cuadrupolos pasivos

Cuadrupolos pasivos elementales

	Resistencia en serie	Admisión paralela	Línea de transmisión	Transformador ideal
Diagrama
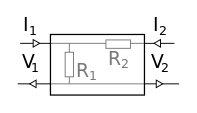
Detalles	Resistencia, o más generalmente impedancia en serie. Reemplace R por una inductancia, por una capacitancia. jLω{\ Displaystyle jL \ omega} 1jVSω{\ Displaystyle {\ frac {1} {jC \ omega}}}	Admisión en paralelo. Reemplace Y por una inductancia, por una capacitancia. 1jLω{\ Displaystyle {\ frac {1} {jL \ omega}}} jVSω{\ Displaystyle jC \ omega}	Línea de transmisión, del tipo coaxial o trenzado por ejemplo. Z0{\ Displaystyle Z_ {0}}es la impedancia característica , la constante de propagación, la longitud de la línea. 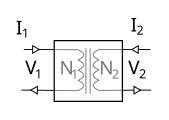γ{\ Displaystyle \ gamma} l{\ Displaystyle l}	Relación de transformador ideal del número de vueltas. metro=NO2NO1{\ Displaystyle m = {\ frac {N_ {2}} {N_ {1}}}}
Configuración de transferencia (ABVSD)={\ displaystyle {\ begin {pmatrix} A&B \\ C&D \ end {pmatrix}} =}	(1R01){\ displaystyle {\ begin {pmatrix} 1 & R \\ 0 & 1 \ end {pmatrix}}}	(10Y1){\ displaystyle {\ begin {pmatrix} 1 & 0 \\ Y & 1 \ end {pmatrix}}}	(aporrear⁡(γl)Z0pecado⁡(γl)pecado⁡(γl)Z0aporrear⁡(γl)){\ Displaystyle {\ begin {pmatrix} \ cosh \ left (\ gamma l \ right) & Z_ {0} \ sinh \ left (\ gamma l \ right) \\ {\ frac {\ sinh \ left (\ gamma l \ right)} {Z_ {0}}} & \ cosh \ left (\ gamma l \ right) \ end {pmatrix}}}	(metro001metro){\ displaystyle {\ begin {pmatrix} m & 0 \\ 0 & {\ frac {1} {m}} \ end {pmatrix}}}
Configuración de transferencia inversa (A′B′VS′D′)={\ displaystyle {\ begin {pmatrix} A '& B' \\ C '& D' \ end {pmatrix}} =}	(1-R01){\ displaystyle {\ begin {pmatrix} 1 & -R \\ 0 & 1 \ end {pmatrix}}}	(10-Y1){\ displaystyle {\ begin {pmatrix} 1 & 0 \\ - Y & 1 \ end {pmatrix}}}	(aporrear⁡(γl)-Z0pecado⁡(γl)-1Z0pecado⁡(γl)aporrear⁡(γl)){\ Displaystyle {\ begin {pmatrix} \ cosh \ left (\ gamma l \ right) y - Z_ {0} \ sinh \ left (\ gamma l \ right) \\ - {\ frac {1} {Z_ {0 }}} \ sinh \ left (\ gamma l \ right) & \ cosh \ left (\ gamma l \ right) \ end {pmatrix}}}	(1metro00metro){\ displaystyle {\ begin {pmatrix} {\ frac {1} {m}} & 0 \\ 0 & m \ end {pmatrix}}}

Atenuadores pasivos

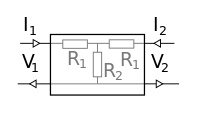
Estos atenuadores son combinaciones de resistencias en serie y en paralelo, por lo que se encuentra fácilmente la descripción de su matriz a partir de las fórmulas anteriores. Observamos la impedancia para la que es adecuado el atenuador y la relación de atenuación deseada. Z0{\ Displaystyle Z_ {0}}K{\ Displaystyle K}

Se define como , por tanto . A partir de y , las fórmulas permiten determinar los valores de las resistencias. K=VInoVotut{\ Displaystyle K = {\ frac {V_ {in}} {V_ {out}}}}K>1{\ Displaystyle K> 1}Z0{\ Displaystyle Z_ {0}}K{\ Displaystyle K}

	Atenuador en forma de L	Atenuador en forma de L, invertido	Π atenuador	Atenuador T
Diagrama
Cálculo de resistencias	R1=Z0K-1K{\ Displaystyle R_ {1} = Z_ {0} {\ frac {K-1} {K}}} R2=Z0K-1{\ Displaystyle R_ {2} = {\ frac {Z_ {0}} {K-1}}}	R1=Z0KK-1{\ Displaystyle R_ {1} = Z_ {0} {\ frac {K} {K-1}}} R2=Z0(K-1){\ Displaystyle R_ {2} = Z_ {0} (K-1)}	R1=Z0K2-12K{\ Displaystyle R_ {1} = Z_ {0} {\ frac {K ^ {2} -1} {2K}}} R2=Z0K+1K-1{\ Displaystyle R_ {2} = Z_ {0} {\ frac {K + 1} {K-1}}}	R1=Z0K-1K+1{\ Displaystyle R_ {1} = Z_ {0} {\ frac {K-1} {K + 1}}} R2=Z02KK2-1{\ Displaystyle R_ {2} = Z_ {0} {\ frac {2K} {K ^ {2} -1}}}
Configuración de transferencia (ABVSD)={\ displaystyle {\ begin {pmatrix} A&B \\ C&D \ end {pmatrix}} =}	(1R101)(10R2-11){\ displaystyle {\ begin {pmatrix} 1 & R_ {1} \\ 0 & 1 \ end {pmatrix}} {\ begin {pmatrix} 1 & 0 \\ R_ {2} ^ {- 1} & 1 \ end {pmatrix}}} =(1+R1R2R1R2-11){\ displaystyle = {\ begin {pmatrix} 1 + {\ frac {R_ {1}} {R_ {2}}} & R_ {1} \\ R_ {2} ^ {- 1} & 1 \ end {pmatrix }}} =(1+(K-1)2KZ0K-1KK-1Z01){\ displaystyle = {\ begin {pmatrix} 1 + {\ frac {(K-1) ^ {2}} {K}} & Z_ {0} {\ frac {K-1} {K}} \\ { \ frac {K-1} {Z_ {0}}} & 1 \ end {pmatrix}}}	(10R1-11)(1R201){\ displaystyle {\ begin {pmatrix} 1 & 0 \\ R_ {1} ^ {- 1} & 1 \ end {pmatrix}} {\ begin {pmatrix} 1 & R_ {2} \\ 0 & 1 \ end {pmatrix}}} =(1R2R1-11+R2R1){\ displaystyle = {\ begin {pmatrix} 1 & R_ {2} \\ R_ {1} ^ {- 1} & 1 + {\ frac {R_ {2}} {R_ {1}}} \ end {pmatrix }}} =(1Z0(K-1)K-1Z0K1+(K-1)2K){\ displaystyle = {\ begin {pmatrix} 1 & Z_ {0} (K-1) \\ {\ frac {K-1} {Z_ {0} K}} & 1 + {\ frac {(K-1) ) ^ {2}} {K}} \ end {pmatrix}}}	(10R2-11)(1R101)(10R2-11){\ displaystyle {\ begin {pmatrix} 1 & 0 \\ R_ {2} ^ {- 1} & 1 \ end {pmatrix}} {\ begin {pmatrix} 1 & R_ {1} \\ 0 & 1 \ end {pmatrix}} {\ begin {pmatrix} 1 & 0 \\ R_ {2} ^ {- 1} & 1 \ end {pmatrix}}} =(1+R1R2R12R2-1+R1R221+R1R2){\ displaystyle = {\ begin {pmatrix} 1 + {\ frac {R_ {1}} {R_ {2}}} & R_ {1} \\ 2R_ {2} ^ {- 1} + {\ frac {R_ {1}} {R_ {2} ^ {2}}} & 1 + {\ frac {R_ {1}} {R_ {2}}} \ end {pmatrix}}} =(1+(K-1)22KZ0K2-12KK2-12Z0K1+(K-1)22K){\ displaystyle = {\ begin {pmatrix} 1 + {\ frac {(K-1) ^ {2}} {2K}} & Z_ {0} {\ frac {K ^ {2} -1} {2K} } \\ {\ frac {K ^ {2} -1} {2Z_ {0} K}} & 1 + {\ frac {(K-1) ^ {2}} {2K}} \ end {pmatrix}} }	(1R101)(10R2-11)(1R101){\ displaystyle {\ begin {pmatrix} 1 & R_ {1} \\ 0 & 1 \ end {pmatrix}} {\ begin {pmatrix} 1 & 0 \\ R_ {2} ^ {- 1} & 1 \ end {pmatrix}} {\ begin {pmatrix} 1 & R_ {1} \\ 0 & 1 \ end {pmatrix}}} =(1+R1R22R1+R12R2R2-11+R1R2){\ displaystyle = {\ begin {pmatrix} 1 + {\ frac {R_ {1}} {R_ {2}}} y 2R_ {1} + {\ frac {R_ {1} ^ {2}} {R_ { 2}}} \\ R_ {2} ^ {- 1} & 1 + {\ frac {R_ {1}} {R_ {2}}} \ end {pmatrix}}} =(1+(K-1)22KZ(K2-1)2KK2-12Z0K1+(K-1)22K){\ displaystyle = {\ begin {pmatrix} 1 + {\ frac {(K-1) ^ {2}} {2K}} y {\ frac {Z (K ^ {2} -1)} {2K}} \\ {\ frac {K ^ {2} -1} {2Z_ {0} K}} & 1 + {\ frac {(K-1) ^ {2}} {2K}} \ end {pmatrix}}}
Configuración de transferencia inversa (A′B′VS′D′)={\ displaystyle {\ begin {pmatrix} A '& B' \\ C '& D' \ end {pmatrix}} =}	(10-R2-11)(1-R101){\ displaystyle {\ begin {pmatrix} 1 & 0 \\ - R_ {2} ^ {- 1} & 1 \ end {pmatrix}} {\ begin {pmatrix} 1 & -R_ {1} \\ 0 & 1 \ end {pmatrix}}} =(1-R1-R2-11+R1R2){\ displaystyle = {\ begin {pmatrix} 1 & -R_ {1} \\ - R_ {2} ^ {- 1} & 1 + {\ frac {R_ {1}} {R_ {2}}} \ end {pmatrix}}} =(1-Z0K-1K-K-1Z01+(K-1)2K){\ displaystyle = {\ begin {pmatrix} 1 & -Z_ {0} {\ frac {K-1} {K}} \\ - {\ frac {K-1} {Z_ {0}}} & 1 + {\ frac {(K-1) ^ {2}} {K}} \ end {pmatrix}}}	(1-R201)(10-R1-11){\ displaystyle {\ begin {pmatrix} 1 & -R_ {2} \\ 0 & 1 \ end {pmatrix}} {\ begin {pmatrix} 1 & 0 \\ - R_ {1} ^ {- 1} & 1 \ end {pmatrix}}} =(1+R2R1-R2-R1-11){\ displaystyle = {\ begin {pmatrix} 1 + {\ frac {R_ {2}} {R_ {1}}} y - R_ {2} \\ - R_ {1} ^ {- 1} y 1 \ end {pmatrix}}} =(1+(K-1)2K-Z0(K-1)-K-1Z0K1){\ displaystyle = {\ begin {pmatrix} 1 + {\ frac {(K-1) ^ {2}} {K}} y - Z_ {0} (K-1) \\ - {\ frac {K- 1} {Z_ {0} K}} & 1 \ end {pmatrix}}}	(10-R2-11)(1-R101)(10-R2-11){\ displaystyle {\ begin {pmatrix} 1 & 0 \\ - R_ {2} ^ {- 1} & 1 \ end {pmatrix}} {\ begin {pmatrix} 1 & -R_ {1} \\ 0 & 1 \ end {pmatrix}} {\ begin {pmatrix} 1 & 0 \\ - R_ {2} ^ {- 1} & 1 \ end {pmatrix}}} =(1+R1R2-R1-2R2-1-R1R221+R1R2){\ displaystyle = {\ begin {pmatrix} 1 + {\ frac {R_ {1}} {R_ {2}}} y - R_ {1} \\ - 2R_ {2} ^ {- 1} - {\ frac {R_ {1}} {R_ {2} ^ {2}}} & 1 + {\ frac {R_ {1}} {R_ {2}}} \ end {pmatrix}}} =(1+(K-1)22K-Z0K2-12K-K2-12Z0K1+(K-1)22K){\ displaystyle = {\ begin {pmatrix} 1 + {\ frac {(K-1) ^ {2}} {2K}} y - Z_ {0} {\ frac {K ^ {2} -1} {2K }} \\ - {\ frac {K ^ {2} -1} {2Z_ {0} K}} & 1 + {\ frac {(K-1) ^ {2}} {2K}} \ end {pmatrix }}}	(1-R101)(10-R2-11)(1-R101){\ displaystyle {\ begin {pmatrix} 1 & -R_ {1} \\ 0 & 1 \ end {pmatrix}} {\ begin {pmatrix} 1 & 0 \\ - R_ {2} ^ {- 1} & 1 \ end {pmatrix}} {\ begin {pmatrix} 1 & -R_ {1} \\ 0 & 1 \ end {pmatrix}}} =(1+R1R2-2R1+-R12R2-R2-11+R1R2){\ displaystyle = {\ begin {pmatrix} 1 + {\ frac {R_ {1}} {R_ {2}}} y - 2R_ {1} + - {\ frac {R_ {1} ^ {2}} { R_ {2}}} \\ - R_ {2} ^ {- 1} & 1 + {\ frac {R_ {1}} {R_ {2}}} \ end {pmatrix}}} =(1+(K-1)22K-Z0(K2-1)2K-K2-12Z0K1+(K-1)22K){\ displaystyle = {\ begin {pmatrix} 1 + {\ frac {(K-1) ^ {2}} {2K}} y - Z_ {0} {\ frac {(K ^ {2} -1)} {2K}} \\ - {\ frac {K ^ {2} -1} {2Z_ {0} K}} & 1 + {\ frac {(K-1) ^ {2}} {2K}} \ end {pmatrix}}}
Parámetro S (S11S12S21S22)={\ displaystyle {\ begin {pmatrix} S_ {11} & S_ {12} \\ S_ {21} & S_ {22} \ end {pmatrix}} =} para Z01=Z02=Z0{\ Displaystyle Z_ {01} = Z_ {02} = Z_ {0}}	(01K1K0){\ displaystyle {\ begin {pmatrix} 0 y {\ frac {1} {K}} \\ {\ frac {1} {K}} y 0 \ end {pmatrix}}}	(01K1K0){\ displaystyle {\ begin {pmatrix} 0 y {\ frac {1} {K}} \\ {\ frac {1} {K}} y 0 \ end {pmatrix}}}	(01K1K0){\ displaystyle {\ begin {pmatrix} 0 y {\ frac {1} {K}} \\ {\ frac {1} {K}} y 0 \ end {pmatrix}}}	(01K1K0){\ displaystyle {\ begin {pmatrix} 0 y {\ frac {1} {K}} \\ {\ frac {1} {K}} y 0 \ end {pmatrix}}}

Tenga en cuenta que todos los atenuadores tienen la misma matriz S: por lo tanto, son equivalentes. Los términos y son cero, lo que expresa la ausencia de una onda reflejada. s11{\ Displaystyle s_ {11}}s22{\ Displaystyle s_ {22}}

Teorema de reciprocidad en cuadrupolos pasivos

El ensamblaje de componentes pasivos básicos (resistencia, inductancia, condensadores) respeta el teorema de reciprocidad, ilustrado anteriormente. Sin embargo, existen componentes pasivos y lineales que, utilizando materiales ferromagnéticos , son no recíprocos y útiles gracias a esta particularidad: circuladores y aislantes .

Cuando un cuadrupolo es recíproco, esta propiedad se encuentra en las matrices que lo parametrizan:

• Las matrices de admitancia e impedancia son simétricas  : Y 12 = Y 21 , Z 12 = Z 21 ,
• En la matriz híbrida: H 12 = -H 21
• El determinante de la matriz de transferencia es igual a 1: y ΔT = AD-BC = 1 .

Cuadrupolo simétrico

Si los dos puertos de un cuadrupolo simétrico son indistinguibles: los índices correspondientes, 1 y 2, de los parámetros de la matriz de impedancia o admitancia son por lo tanto permutables sin cambios. En consecuencia, para cuadrupolos simétricos, además de tener las propiedades de reciprocidad, tenemos las relaciones Y 11 = Y 22 y Z 11 = Z 22 .

Cuadrupolos activos

Llamamos activo a un circuito que tiene la capacidad de aportar energía adicional.

Transistor bipolar

La aproximación de pequeña señal de un transistor bipolar es comúnmente modelada por el circuito equivalente en pi arriba. Este circuito es un cuadrupolo activo, cuya configuración es la siguiente. Cabe señalar que aquí las magnitudes estudiadas no son las corrientes y tensiones totales, físicamente presentes en los terminales de los transistores, sino solo su variación alrededor de un punto de polarización. En un modelo ligeramente simplificado donde y se omiten (cero e infinito respectivamente), el cuadrupolo activo se representa mediante la siguiente parametrización de hidruros, utilizando las mismas notaciones que en el diagrama: rBB{\ Displaystyle r_ {bb}}rB′vs{\ Displaystyle r_ {b'c}}

(VBIVS)=1GRAMOπ+jω(VSπ+VSμ)(1jωVSμgramometro-jωVSμq(jω))(IBVVS){\ Displaystyle {V_ {B} \ elija I_ {C}} = {\ frac {1} {G _ {\ pi} + j \ omega (C _ {\ pi} + C _ {\ mu})}} {\ begin {pmatrix} 1 & j \ omega C _ {\ mu} \\ g_ {m} -j \ omega C _ {\ mu} & q (j \ omega) \ end {pmatrix}} {I_ {B } \ elija V_ {C}}} Con : q(jω)=GRAMOπ+jω(VSπ)(GRAMO0+jω(VSμ))+jω(VSμ)(GRAMOπ+gramometro){\ Displaystyle q (j \ omega) = G _ {\ pi} + j \ omega (C _ {\ pi}) (G_ {0} + j \ omega (C _ {\ mu})) + j \ omega (C_ {\ mu}) (G _ {\ pi} + g_ {m})}

Transistor de efecto de campo

De manera similar, un transistor MOSFET utilizado como una pequeña señal alrededor de un punto de polarización es modelado por el circuito pi de arriba. Aquí, la configuración Z es la más conveniente:

(VGRAMOSVDS)=(1jω(VSgramos)0-gramometror0jω(VSgramos)-r0)(IGRAMOID){\ displaystyle {V_ {GS} \ choose V_ {DS}} = {\ begin {pmatrix} {\ frac {1} {j \ omega (C_ {g} s)}} & 0 \\ {\ frac {- g_ {m} r_ {0}} {j \ omega (C_ {g} s)}} & - r_ {0} \ end {pmatrix}} {I_ {G} \ choose I_ {D}}}

Amplificador

En el ejemplo de un amplificador inversor de voltaje , la matriz ABCD se escribe de la siguiente manera (las corrientes se indican positivamente hacia el interior del conjunto):

(VmiImi)=(-R1R20-1R20)(Vs-Is){\ displaystyle {V_ {e} \ elija I_ {e}} = {\ begin {pmatrix} - {\ frac {R_ {1}} {R_ {2}}} & 0 \\ - {\ frac {1} {R_ {2}}} & 0 \ end {pmatrix}} {V_ {s} \ choose -I_ {s}}},

El determinante de esta matriz es cero: de hecho, tal ensamblaje no respeta el teorema de reciprocidad. Físicamente, los dos ceros de la derecha significan que la corriente puede cambiar sin influir en los valores de entrada. Is{\ Displaystyle I_ {s}}

Operaciones de cuadrupolo

Impedancias de entrada y salida

Aquí representamos un cuadrupolo interpuesto entre un generador Thévenin y una impedancia de carga. Entonces podemos estar interesados ​​en:

• A la impedancia "vista" por el generador, y que representa el cuadripolo más su carga.
• Al generador equivalente "visto" por la carga y que representa el generador y el cuadrupolo.ZL{\ Displaystyle Z_ {L}}

Para el primer problema, al cargar el cuadripolo con la carga , se impone: (el signo menos se debe a las convenciones de dirección de las corrientes). Esta restricción elimina cierto grado de libertad del sistema. ZL{\ Displaystyle Z_ {L}}V2=-ZLI2{\ Displaystyle V_ {2} = - Z_ {L} I_ {2}}

Reanudando el ajuste de impedancia del cuadrupolo: (V1V2)=(Z11Z12Z21Z22)(I1I2){\ Displaystyle {V_ {1} \ choose V_ {2}} = {\ begin {pmatrix} Z_ {11} & Z_ {12} \\ Z_ {21} & Z_ {22} \ end {pmatrix}} {I_ {1} \ elija I_ {2}}} se convierte en : (V1-ZLI2)=(Z11Z12Z21Z22)(I1I2){\ Displaystyle {V_ {1} \ choose -Z_ {L} I_ {2}} = {\ begin {pmatrix} Z_ {11} & Z_ {12} \\ Z_ {21} & Z_ {22} \ end { pmatrix}} {I_ {1} \ choose I_ {2}}}

La segunda línea permite expresar en función de , y sustituyendo en la primera, se obtiene la relación entre y , es decir la impedancia de carga formada por el cuadripolo y . I2{\ Displaystyle I_ {2}}I1{\ Displaystyle I_ {1}}V1{\ Displaystyle V_ {1}}I1{\ Displaystyle I_ {1}}ZL{\ Displaystyle Z_ {L}}

V1=Z11I1-Z12Z21ZL+Z22I1{\ Displaystyle V_ {1} = Z_ {11} I_ {1} - {\ frac {Z_ {12} Z_ {21}} {Z_ {L} + Z_ {22}}} I_ {1}} V1=(Z11-Z12Z21ZL+Z22)I1=ZInoI1{\ Displaystyle V_ {1} = \ izquierda (Z_ {11} - {\ frac {Z_ {12} Z_ {21}} {Z_ {L} + Z_ {22}}} \ derecha) I_ {1} = Z_ {\ mathrm {in}} I_ {1}}

Función de transferencia

Tomando nuevamente el diagrama anterior y sus notaciones, uno se interesa en la función de transferencia , conociendo los parámetros ABCD del cuadrupolo:

Ft=V2V0=ZLAZL+B+VSZLZS+DZS{\ displaystyle F_ {t} = {\ frac {V_ {2}} {V_ {0}}} = {\ frac {Z_ {L}} {AZ_ {L} + B + CZ_ {L} Z_ {S} + DZ_ {S}}}}

Asociación de dos cuadrupolos

Se pueden combinar dos cuadrupolos (para formar uno nuevo) de cinco formas diferentes. En cada caso, uno de los ajustes es muy adecuado, porque permite obtener la matriz del nuevo cuadrupolo obtenido mediante una simple operación a partir de las matrices que representan los dos cuadripolos de partida.

Designacion	Diagrama	Propiedades
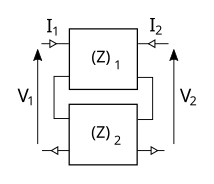
Serie		Z=Z1+Z2{\ Displaystyle {Z} = {Z_ {1}} + {Z_ {2}}} Se agregan las matrices de impedancia.
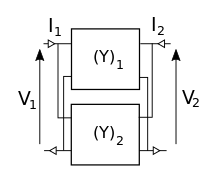
Paralelo		Y=Y1+Y2{\ Displaystyle {Y} = {Y_ {1}} + {Y_ {2}}} Se agregan matrices de admisión.
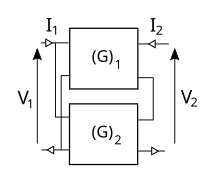
Serie paralela		GRAMO=GRAMO1+GRAMO2{\ Displaystyle {G} = {G_ {1}} + {G_ {2}}} Se agregan las matrices híbridas inversas.
Serie-paralelo		H=H1+H2{\ Displaystyle {H} = {H_ {1}} + {H_ {2}}} Se agregan matrices híbridas.
cascada		T=T1×T2{\ Displaystyle {T} = {T_ {1}} \ times {T_ {2}}} T′=T2′×T1′{\ Displaystyle {T '} = {T' _ {2}} \ times {T '_ {1}}} Las matrices de transferencia se multiplican. La dirección de la multiplicación es diferente para T y T ': el producto de la matriz es generalmente no conmutativo .

Caracterización experimental

El analizador de redes es un instrumento dedicado específicamente a medir los parámetros S de un cuadrupolo. El instrumento tiene dos salidas coaxiales que le permiten medir los términos de la matriz S.

Fuera de la electrónica

La analogía electromecánica permite el uso del formalismo cuadrupolo para sistemas mecánicos o electromecánicos. En este caso, los dos puertos, o solo uno, presentan, en sustitución de las cantidades de corriente y tensión eléctricas, un par de cantidad mecánica ( fuerza y velocidad, presión y velocidad, par y velocidad angular según el sistema estudiado).

Así, el estudio de transductores piezoeléctricos , en una aproximación unidimensional, recurre a circuitos equivalentes formados por cuadrupolos. Los dos circuitos más comunes son los de Mason y KLM . En cada uno de estos circuitos, el efecto piezoeléctrico está representado por un cuadrupolo cuya entrada es eléctrica, y cuya salida es la velocidad y presión (o fuerza) en el centro de la capa piezoeléctrica, mientras que cada capa es un cuadrupolo mecánico, correspondiente a un línea de transmisión.

Notas y referencias

1. Comisión Electrotécnica Internacional , Vocabulario Electrotécnico Internacional ISO 60050 , 1987/2019 ( leer en línea ) , p.  131-12-66 Teoría de circuitos: cuadrupolo.
2. Tahar Neffati , Electrónica de la A a la Z , París, Dunod ,2006, p.  240-245 "cuadrupolo".
3. Richard C. Dorf y James A. Svoboda, Introducción a los circuitos eléctricos , John Wiley & Sons ,7 de enero de 2010, 886  p. ( ISBN  978-0-470-52157-1 , leer en línea )
4. (en) GG Johnstone y JHB Deane , "  Relations entre two port parameters  " , International Journal of Electronics , vol.  71, n o  1,Julio de 1991, p.  107-116 ( ISSN  0020-7217 y 1362-3060 , DOI  10.1080 / 00207219108925462 , leer en línea , consultado el 19 de marzo de 2019 )
5. S. Sercu y L. Martens , “  paquetes N-portuarias caracterización y las interconexiones con un analizador de red de 2 puertos  ”, rendimiento eléctrico del Electronic Packaging , IEEE,1997, p.  163-166 ( ISBN  9780780342033 , DOI  10.1109 / EPEP.1997.634062 , leído en línea , consultado el 22 de marzo de 2019 )
6. DA Frickey , “  Conversiones entre los parámetros S, Z, Y, H, ABCD y T que son válidos para impedancias de carga y fuente complejas  ”, Transacciones IEEE sobre teoría y técnicas de microondas , vol.  42, n o  2Febrero de 1994, p.  205–211 ( DOI  10.1109 / 22.275248 , leído en línea , consultado el 22 de marzo de 2019 )
7. Todo sobre circuitos, libro de texto
8. (en) Negar Reiskarimian y Harish Krishnaswamy , "  La no reciprocidad libre magnética es conmutación escalonada  " , Nature Communications , vol.  7, n o  1,diciembre de 2016( ISSN  2041-1723 , PMID  27079524 , PMCID  PMC4835534 , DOI  10.1038 / ncomms11217 , leído en línea , consultado el 24 de marzo de 2019 )
9. Ingeniería Eléctrica e Informática 142 de dos puertos Redes y amplificadores AM Niknejad (Berkeley Curso)
10. ECE 580 - Teoría de redes, Universidad Estatal de Oregon
11. (in) S. Sherritt , SP Leary , BP Dolgin e Y. Bar-Cohen , "  Comparación de los circuitos equivalentes de Mason y KLM para resonadores piezoeléctricos en la moda de espesor  " , 1999 IEEE Ultrasonics Symposium. Actas. Simposio internacional , vol.  2,1999, p.  921–926 ( DOI  10.1109 / ULTSYM.1999.849139 ).

Ver también

• Diagramas de Bode
• Filtro (electrónico)
• Teorema de Kennelly
• Parámetros S