Proceso de Galton-Watson

El proceso de ramificación (o proceso de Bienaymé-Galton-Watson ) es un proceso estocástico utilizado para describir la dinámica de la población .

Histórico

Originalmente, este modelo fue introducido por Bienaymé en 1845 e independientemente por Galton en 1873 para estudiar la desaparición de los apellidos .

Supongamos que cada varón adulto transmite su apellido a cada uno de sus hijos. Supongamos también que el número de hijos de cada hombre es una variable aleatoria entera (y que la distribución de probabilidad es la misma para todos los hombres de un linaje ). Por lo tanto, un patronímico cuyos portadores tienen un número de hijos estrictamente inferior a 1 en promedio está destinado a desaparecer. Por el contrario, si el número medio de hijos es superior a 1, entonces la probabilidad de supervivencia de este nombre es distinta de cero y, en caso de supervivencia, el número de portadores del apellido crece exponencialmente.

Formulación general

Se asume que existe una población de individuos que se reproducen de forma independiente. Cada individuo i da a luz a individuos y muere. Suponemos que son variables aleatorias independientes con valores enteros siguiendo la distribución Por ejemplo, $X_ {i}$ $X_ {i}$ ${\ Displaystyle p = \ left (p_ {k} \ right) _ {k \ in \ mathbb {N}}.}$

si, con probabilidad , el individuo i muere sin reproducirse; ${\ Displaystyle p_ {0} = \ mathbb {P} (X_ {i} = 0),}$ ${\ Displaystyle X_ {i} = 0,}$

si, con probabilidad, entonces hay un reemplazo uno por uno del individuo i ; ${\ Displaystyle p_ {1} = \ mathbb {P} (X_ {i} = 1),}$ ${\ Displaystyle X_ {i} = 1,}$

etc.

Notación : la función generadora asociada con la distribución de probabilidad definida por: $\ varphi,$ ${\ Displaystyle p = \ left (p_ {k} \ right) _ {k \ in \ mathbb {N}},}$

{\ Displaystyle \ varphi (s) \ = \ \ sum _ {n \ geq 0} \, p_ {n} \, s ^ ​​{n} \ = \ \ mathbb {E} \ left [s ^ {X_ {i}} \ derecha],}

es de particular importancia en la discusión de los resultados esenciales de los procesos de Galton-Watson.

Parámetro crítico y clasificación de los procesos de Galton-Watson

Tenga en cuenta el tamaño de la población en la enésima generación. A menudo se asume que la población tiene un solo ancestro , lo que resulta en $Z_ {n}$

{\ Displaystyle Z_ {0} = 1.}

El número

{\ Displaystyle m \ = \ \ sum _ {k} kp_ {k} \ = \ \ varphi ^ {\ prime} (1)}

denota el número medio de hijos de un individuo típico de la población considerada. La evolución del tamaño medio de la población se rige por la siguiente fórmula de recurrencia, consecuencia de la fórmula de Wald :

{\ Displaystyle \ mathbb {E} [Z_ {n + 1}] \ = \ m \ \ mathbb {E} [Z_ {n}],}

de lo que se sigue que

{\ Displaystyle \ mathbb {E} [Z_ {n}] \ = \ m ^ {n}.}

Definición - Si, a partir de cierto rango, todos los términos de la secuencia son cero, decimos que hay extinción de la población. ${\ Displaystyle \ left (Z_ {n} \ right) _ {n \ geq 0}}$

Clasificación de los procesos de Galton-Watson : hay dos regímenes separados por un valor crítico del parámetro : $metro$

Si se dice que el proceso de Galton-Watson es subcrítico . La extinción de la población ocurre con probabilidad 1; ${\ Displaystyle m <1,}$

Si se dice que el proceso de Galton-Watson es demasiado crítico . Entonces, la probabilidad de supervivencia de este nombre no es cero (la probabilidad de extinción es estrictamente menor que 1). En caso de supervivencia, el número de portadores del apellido crece exponencialmente. ${\ displaystyle m> 1,}$

Si, entonces se dice que el proceso de Galton-Watson es crítico . Su comportamiento es más complejo y se discutirá más adelante. ${\ Displaystyle m = 1,}$

Notación de sobrino

La notación de Neveu permite una descripción rigurosa de la evolución de la población utilizando un árbol plano enraizado , que es de hecho el árbol genealógico de esta población. Este árbol plano enraizado se puede describir sin ambigüedades por la lista de sus vértices, cada uno designado por una serie finita de números enteros, que son las posiciones, dentro de sus hermanos, de los antepasados (o ascendentes) de este vértice: el vértice 2 | 4 | 3 designa el 3 rd hijo del 4 º hijo de la 2 nd hijo del ancestro (el antepasado sí mismo siendo designan a continuación vaciar, observado ). Por convención, el antepasado es el vértice inicial del borde de la raíz y el vértice final del borde de la raíz es el hijo mayor del antepasado: como tal, por lo tanto, se denota por 1 . La longitud de la secuencia asociada a un vértice es la altura (o profundidad ) del vértice, es decir, la distancia entre este vértice y el comienzo de la raíz, que representa al antepasado: siguiendo la metáfora , un vértice de altura n representa una individuo perteneciente a la enésima generación de la población fundada por el antepasado. Los 5 árboles con 3 aristas: $\ conjunto vacio$

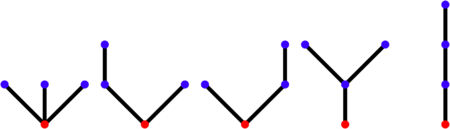
son descritos por los 5 conjuntos de palabras

{\ Displaystyle \ {\ conjunto vacío, 1,2,3 \}, \ \ {\ conjunto vacío, 1,11,2 \}, \ \ {\ conjunto vacío, 1,2,21 \}, \ \ {\ conjunto vacío, 1,11,12 \}, \ \ {\ conjunto vacío, 1,11,111 \}.}

Con esta notación, un árbol plano codifica convenientemente una realización del proceso de Galton-Watson con extinción: este árbol se llama entonces árbol de Galton-Watson . Nada se opone a definir un árbol plano infinito utilizando la notación de Neveu, que permite codificar las realizaciones de los procesos de Galton-Watson donde la población no se extingue.

Ejemplo:

El árbol de la figura opuesta corresponde a una serie de variables aleatorias definidas de la siguiente manera: ${\ Displaystyle X_ {i},}$

{\ Displaystyle (X _ {\ emptyset}, X_ {1}, X_ {2}, X_ {3}, X_ {11}, X_ {12}, X_ {111}, X_ {121}, X_ {122} , \ puntos) \ = \ (3,2,0,0,1,2,1,0,1, \ puntos).}

Así, un proceso de Galton-Watson puede verse como un funcional determinista de una familia de variables aleatorias independientes y de la misma ley la variable que designa la descendencia del individuo i (el número de hijos a los que dan a luz al morir). Aquí denota el conjunto (contable) de secuencias de números enteros de longitudes finitas (posiblemente de longitud cero en el caso de ): ${\ Displaystyle \ left (X_ {i} \ right) _ {i \ in \ mathbb {N} ^ {\ star}}}$ ${\ Displaystyle p = \ left (p_ {k} \ right) _ {k \ in \ mathbb {N}},}$ $X_ {i}$ ${\ Displaystyle \ mathbb {N} ^ {\ star}}$ $\ conjunto vacio$

{\ Displaystyle \ mathbb {N} ^ {\ star} = \ {\ juego vacío \} \ cup \ mathbb {N} \ cup \ mathbb {N} ^ {2} \ cup \ mathbb {N} ^ {3} \ taza \ puntos}

Ejemplo:

Algunas variables aleatorias en la secuencia no influyen en el proceso de Galton-Watson: en el ejemplo opuesto, o no tienen importancia porque el antepasado tiene estrictamente menos de 4 hijos ( ) y el individuo 12 tiene estrictamente menos de 6 hijos ( ). De manera similar individuos descendencia de la 5 ª generación ( correspondiente a suites i longitud 5) no influyen en la realización del proceso de Galton-Watson como la población murió en el 4 ° generación ( ). ${\ Displaystyle \ left (X_ {i} \ right) _ {i \ in \ mathbb {N} ^ {\ star}}}$ ${\ Displaystyle X_ {4}}$ ${\ Displaystyle X_ {126}}$ ${\ Displaystyle X _ {\ emptyset} = 3}$ ${\ Displaystyle X_ {12} = 2}$ $X_ {i}$ ${\ Displaystyle X_ {1111} = X_ {1221} = 0}$

Estudio detallado del tamaño de las generaciones

Tenga en cuenta la función generadora de la variable aleatoria definida por $\ varphi _ {n}$ ${\ Displaystyle Z_ {n},}$

{\ Displaystyle \ varphi _ {n} (s) \ = \ \ sum _ {k \ geq 0} \, \ mathbb {P} (Z_ {n} = k) \, s ^ ​​{k} \ = \ \ mathbb {E} \ left [s ^ {Z_ {n}} \ right].}

Vamos a posar

{\ Displaystyle p _ {\ ell} ^ {\ star k} \ = \ [s ^ {\ ell}] \ varphi ^ {k} (s) \ = \ \ mathbb {P} (X_ {1} + \ puntos + X_ {k} = \ ell),}

donde las X i son variables aleatorias independientes, todas de derecho ; es el k- ésimo poder convolucional de la ley $pag$ ${\ Displaystyle p ^ {\ star k} = \ left (p _ {\ ell} ^ {\ star k} \ right) _ {\ ell \ geq 0}}$ $pag.$

En virtud de la propiedad de composición de las funciones generadoras , tenemos la siguiente relación:

Relación fundamental de recurrencia -

{\ Displaystyle \ varphi _ {n + 1} \ = \ \ varphi _ {n} \ circ \ varphi.}

Demostración

Para poder aplicar la propiedad de composición de las funciones generadoras , es necesario estar convencido de que (el número de la n + 1ª generación) tiene la misma ley que la suma de variables aleatorias independientes, todas de ley e independientes de por supuesto, es la suma de la descendencia de los individuos pertenecientes a la n º generación, pero, a diferencia del contexto de la propiedad de la composición de generación de funciones , no elegimos los primeros términos de una sucesión de variables aleatorias iid indexado por : la calificación Neveu , por ejemplo, se indexa la secuencia de variables aleatorias iid y las variables de la secuencia que intervienen en la suma se eligen de acuerdo con la historia completa de la población, hasta la n -ésima generación (no incluida). Una vez que estamos convencidos de que, a pesar de esto, (el número de la n + 1ª generación) tiene la misma ley que la suma de variables aleatorias independientes, todas de ley e independientes de, deducimos que ${\ Displaystyle Z_ {n + 1}}$ ${\ Displaystyle Z_ {n}}$ ${\ Displaystyle p,}$ ${\ Displaystyle Z_ {n}.}$ ${\ Displaystyle Z_ {n + 1}}$ ${\ Displaystyle Z_ {n}}$ ${\ Displaystyle Z_ {n}}$ $\ mathbb {N}$ ${\ Displaystyle \ mathbb {N} ^ {n},}$ ${\ Displaystyle Z_ {n}}$ ${\ Displaystyle Z_ {n + 1}}$ ${\ Displaystyle Z_ {n}}$ ${\ Displaystyle p,}$ ${\ Displaystyle Z_ {n},}$

{\ Displaystyle \ varphi _ {n + 1} \ = \ \ varphi _ {n} \ circ \ varphi.}

Demostración

Un enunciado preciso utiliza la noción de ley condicional : para poder aplicar la propiedad de composición de funciones generadoras , debemos verificar que, para cualquier k , la ley condicional de conocer el evento es la ley de la suma de k independientes variables aleatorias, toda la ley descrita por Para verificar esto, tenemos que calcular la ley condicional conociendo un evento más preciso que, es decir, conociendo la composición exacta de la n -ésima generación. Sea L un conjunto de elementos de Denotemos el evento: ${\ Displaystyle Z_ {n + 1}}$ ${\ Displaystyle \ {Z_ {n} = k \}}$ ${\ Displaystyle p,}$ ${\ Displaystyle \ left (p _ {\ ell} ^ {\ star k} \ right) _ {\ ell \ geq 0}.}$ ${\ Displaystyle \ {Z_ {n} = k \},}$ ${\ Displaystyle \ mathbb {N} ^ {n}.}$ ${\ Displaystyle A_ {L}}$

{\ displaystyle A_ {L} \ = \ \ {{\ mathrm {los ~ individuos ~ que forman ~ el ~} n \, \ mathrm {- {\ grave {e}} me ~ g {\ sharp {e}} n La {\ aguda {e}} ración ~ de ~ la ~ población ~ son ~ exactamente ~ los ~ {\ agudos {e}} los {\ agudos {e}} elementos ~ de ~} L} \}.}

En particular, se conocen los ancestros de los individuos pertenecientes a L , proporcionando así información sobre las generaciones 1, 2, ... hasta la generación n-1 . Observamos que el evento pertenece a la tribu generada por la familia de donde i es una secuencia de longitud menor o igual a n-1 . Por otro lado, ${\ Displaystyle A_ {L}}$ ${\ Displaystyle A_ {L}}$ ${\ Displaystyle X_ {i},}$

{\ Displaystyle \ mathbb {P} \ left (Z_ {n + 1} = \ ell \, | \, A_ {L} \ right) = \ mathbb {P} \ left (\ left \ {\ sum _ {j \ in L} X_ {j} \ = \ \ ell \ right \} \ \ cap A_ {L} \ right) \ left (\ mathbb {P} (A_ {L}) \ right) ^ {- 1}}

Dado que L es disjunto del conjunto de secuencias de longitud menor o igual que n-1 , el lema de agrupación implica que

{\ Displaystyle \ mathbb {P} \ left (Z_ {n + 1} = \ ell \, | \, A_ {L} \ right) = \ mathbb {P} \ left (\ sum _ {j \ in L} X_ {j} \ = \ \ ell \ right) = p _ {\ ell} ^ {\ star | L |}.}

Esta última probabilidad depende pero, sobre todo, depende de L solo a través de su cardinal Entonces, en cuanto ${\ Displaystyle \ ell,}$ ${\ Displaystyle | L | = Z_ {n}.}$ ${\ Displaystyle | L | = k,}$

{\ Displaystyle \ mathbb {P} \ left (Z_ {n + 1} = \ ell \, | \, A_ {L} \ right) = \ mathbb {P} \ left (Z_ {n + 1} = \ ell \, | \, Z_ {n} = k \ right) = p _ {\ ell} ^ {\ star | L |},}

en virtud de una variante de la fórmula de probabilidad total . Por cierto, esto muestra que la secuencia tiene la propiedad de Markov . Más precisamente, es una cadena de Markov homogénea de probabilidad de transición. ${\ Displaystyle (Z_ {n}) _ {n \ geq 0}}$ ${\ Displaystyle \ left (p _ {\ ell} ^ {\ star k} \ right) _ {k, \ ell \ geq 0}.}$

Darse cuenta de que

{\ Displaystyle \ varphi _ {0} \ = \ {\ text {Id}},}

deducimos, por inducción, que

{\ Displaystyle \ varphi _ {n} \ = \ \ varphi ^ {\ circ n},}

luego la relación de recurrencia fundamental. También podemos obtener esta relación de manera más directa, descomponiendo de manera diferente (como la suma de X copias de en lugar de como la suma de copias de X ). ${\ Displaystyle Z_ {n + 1}}$ ${\ Displaystyle Z_ {n}}$ ${\ Displaystyle Z_ {n}}$

Notas:

La relación de recurrencia sobre la expectativa de ${\ Displaystyle Z_ {n},}$

{\ Displaystyle \ mathbb {E} [Z_ {n + 1}] \ = \ \ varphi ^ {\ prime} \ left (1 \ right) \ \ mathbb {E} [Z_ {n}],}

luego se sigue de la fórmula para la derivación de funciones compuestas .

Usando la relación de recurrencia fundamental , también encontramos, si es necesario, una fórmula de recurrencia para la varianza de ${\ Displaystyle Z_ {n}.}$
La prueba de la fórmula de inducción fundamental también muestra (módulo algunas modificaciones) que la secuencia es una cadena de Markov cuya matriz de transición está definida por ${\ Displaystyle (Z_ {n}) _ {n \ geq 0}}$ ${\ Displaystyle \ left (p_ {i, j} \ right) _ {i, j \ geq 0}}$ ${\ Displaystyle p_ {k, \ ell} \, = \, p _ {\ ell} ^ {\ star k}.}$

Caso demasiado crítico

En el caso demasiado crítico, el tamaño de la población crece exponencialmente en un conjunto bastante grande.

Teorema : si la ley de la descendencia es integrable, con media m > 1, entonces existe una variable aleatoria M tal que, casi con seguridad,

{\ Displaystyle \ lim \ {\ dfrac {Z_ {n}} {m ^ {n}}} \ = \ M.}

Si, además, la ley de la descendencia es cuadrática integrable, entonces además, converge a M en L 2 . ${\ Displaystyle \ mathbb {P} (M> 0)> 0.}$ ${\ Displaystyle {\ dfrac {Z_ {n}} {m ^ {n}}}}$

Se pueden obtener resultados más precisos gracias al teorema de Kesten-Stigum .

Demostración

Sea una familia independiente e idénticamente distribuida de variables aleatorias de distribución , de media . Definimos filtración: ${\ Displaystyle (X_ {i, j}) _ {i, j}}$ ${\ Displaystyle (p_ {k}) _ {k}}$ ${\ Displaystyle m \> \ 1}$

{\ Displaystyle {\ mathcal {F}} _ {n} \ = \ \ sigma (X_ {i, j}, i \ in \ mathbb {N}, j \ leq n).}

Entonces el proceso definido por inducción por:

{\ Displaystyle Z_ {0} \ = \ 1,}

{\ Displaystyle Z_ {n + 1} \ = \ \ sum _ {i = 1} ^ {Z_ {n}} X_ {i, n + 1}}

es un proceso de Galton-Watson de ley de reproducción . Luego definimos el proceso: ${\ Displaystyle (p_ {k}) _ {k}}$

{\ Displaystyle M_ {n} = {\ dfrac {Z_ {n}} {m ^ {n}}},}

que es una - martingala . En efecto, ${\ mathcal {F}} _ {n}$

{\ Displaystyle {\ begin {alineado} \ mathbb {E} \ left [Z_ {n + 1} \ left | {\ mathcal {F}} _ {n} \ right. \ right] & = \ mathbb {E} \ left [\ sum _ {i = 1} ^ {Z_ {n}} X_ {i, n + 1} \ left | {\ mathcal {F}} _ {n} \ right. \ right] \\ & = \ sum _ {i = 1} ^ {Z_ {n}} \ mathbb {E} \ left [X_ {i, n + 1} \ left | {\ mathcal {F}} _ {n} \ right. \ right ] \\ & = mZ_ {n}, \ end {alineado}}}

lo que resulta en

{\ Displaystyle \ mathbb {E} \ left [M_ {n + 1} \ left | {\ mathcal {F}} _ {n} \ right. \ right] = M_ {n}.}

Como es una martingala positiva, es casi seguro que converja en una variable aleatoria real. $M_ {n}$ $Señor.$

Si además asumimos eso , podemos demostrar que el conjunto es de medida positiva, y que es casi seguro que es igual al conjunto de no extinción del árbol De hecho, en este caso, un cálculo por inducción muestra que está acotado en We entonces deducir la convergencia de versos . Entonces tenemos, en particular, ${\ Displaystyle \ mathbb {E} [X_ {i, j} ^ {2}] \ <\ infty}$ ${\ Displaystyle \ {\ omega \ in \ Omega \, | \, M (\ omega) \> \ 0 \}}$ ${\ Displaystyle \ {\ liminf Z_ {n} \> \ 0 \}.}$ ${\ Displaystyle M_ {n}}$ ${\ Displaystyle L ^ {2}.}$ $L ^ 2$ $M_ {n}$ $METRO$

{\ Displaystyle \ mathbb {E} [M] = \ lim _ {n} \ mathbb {E} [M_ {n}] = \ mathbb {E} [M_ {0}] = \ mathbb {E} [Z_ { 0}] = 1.}

En consecuencia, en un conjunto de medidas distintas de cero. ${\ Displaystyle M \> \ 0}$

Entonces, casi con certeza, es una buena aproximación, al primer orden, del número de individuos de la generación al menos en el conjunto que tiene una probabilidad distinta de cero. ${\ Displaystyle m ^ {n} M (\ omega)}$ ${\ Displaystyle Z_ {n} (\ omega)}$ ${\ Displaystyle n,}$ ${\ Displaystyle \ {\ omega \ in \ Omega \, | \, M (\ omega) \> \ 0 \},}$

Un cálculo explícito

Hay bastantes ejemplos en los que la fórmula de recurrencia fundamental conduce a un cálculo explícito de El ejemplo más conocido es aquel en el que la ley de reproducción es una mezcla de la masa de Dirac en 0 y la ley geométrica , ${\ Displaystyle \ varphi _ {n}.}$

{\ Displaystyle \ mathbb {P} (X_ {i} = k) \ = \ \ alpha 1 \! \! 1_ {k = 0} + (1- \ alpha) (1-p) ^ {k-1} p \, 1 \! \! 1_ {k \ geq 1}, \ quad (\ alpha, p) \ in [0,1] \ times] 0,1],}

de esperanza

{\ Displaystyle m \ = \ \ mathbb {E} [X_ {i}] \ = \ {\ frac {1- \ alpha} {p}}.}

Esto corresponde exactamente a las funciones generadoras que son homografías : $\ varphi$

{\ Displaystyle \ varphi (s) \ = \ \ alpha \ + \ (1- \ alpha) \ {\ frac {ps} {1- (1-p) s}}.}

De acuerdo con la clasificación de homografías en función del número de puntos fijos, la homografía se combina con mapeos cuyas iteraciones se calculan simplemente, es decir a en casos no críticos (dos puntos fijos, 1 y ) y a en el caso crítico ( un punto fijo doble, 1). $\ varphi$ ${\ displaystyle x \ \ rightarrow \ x / m}$ ${\ displaystyle {\ tfrac {\ alpha} {1-p}}}$ ${\ Displaystyle x \ \ rightarrow \ x + c}$

Caso no crítico

Tan pronto como encontremos, por diagonalización de un mapa lineal asociado a la homografía ${\ Displaystyle \ alpha \ neq 1-p,}$ $\ varphi,$

{\ Displaystyle {\ frac {\ varphi (s) - {\ tfrac {\ alpha} {1-p}}} {\ varphi (s) -1}} \ = \ {\ frac {p} {1- \ alpha}} \ {\ frac {s - {\ tfrac {\ alpha} {1-p}}} {s-1}} \ = \ {\ frac {1} {m}} \ {\ frac {s- {\ tfrac {\ alpha} {1-p}}} {s-1}},}

lo que provoca

{\ Displaystyle {\ frac {\ varphi _ {n} (s) - {\ tfrac {\ alpha} {1-p}}} {\ varphi _ {n} (s) -1}} \ = \ {\ frac {1} {m ^ {n}}} \ {\ frac {s - {\ tfrac {\ alpha} {1-p}}} {s-1}},}

y conduce a un cálculo explícito de ${\ Displaystyle \ varphi _ {n}.}$

Caso critico

El caso es el caso crítico que encontramos, siempre razonando sobre un mapa lineal (no diagonalizable) asociado a la homografía ${\ Displaystyle \ alpha = 1-p}$ ${\ Displaystyle m = 1.}$ $\ varphi,$

{\ Displaystyle {\ frac {\ varphi (s) +1} {\ varphi (s) -1}} \ = \ {\ frac {s + 1} {s-1}} \ + \ 2 \ {\ tfrac {p-1} {p}} \ = \ {\ frac {s + 1} {s-1}} \ + \ c,}

Entonces

{\ Displaystyle {\ frac {\ varphi _ {n} (s) +1} {\ varphi _ {n} (s) -1}} \ = \ {\ frac {s + 1} {s-1}} \ + \ nc.}

Finalmente es una homografía: $\ varphi _ {n}$

{\ Displaystyle \ varphi _ {n} (s) \ = \ {\ frac {(nc + 2) s-nc} {ncs + 2-nc}},}

que corresponde a la siguiente elección de parámetros : ${\ Displaystyle (\ alpha _ {n}, p_ {n})}$

{\ Displaystyle p_ {n} = {\ frac {p} {p + n (1-p)}} = \ mathbb {P} (Z_ {n}> 0) = \ mathbb {P} (T> n) , \; \ alpha _ {n} = 1-p_ {n}.}

Aquí T denota la fecha de extinción , es decir, el número de la primera generación vacía.

Probabilidad de extinción

Teorema : la probabilidad de extinción de un proceso de Galton-Watson con una distribución de descendencia es la solución más pequeña, en el intervalo [0,1] , de la ecuación: ${\ Displaystyle \ mathbb {P} ({\ mathcal {E}})}$ ${\ Displaystyle p = \ left (p_ {k} \ right) _ {k \ in \ mathbb {N}},}$

{\ Displaystyle \ varphi (s) \ = \ s.}

Demostración

Esto resulta de lo que

{\ Displaystyle {\ mathcal {E}} \ = \ \ bigcup _ {n \ geq 0} \ {Z_ {n} = 0 \} \ quad {\ text {y}} \ quad \ left \ {\ {Z_ {n} = 0 \} \ Flecha derecha \ {Z_ {n + 1} = 0 \} \ derecha \},}

de donde se sigue, por propiedad del límite creciente , que

{\ Displaystyle \ mathbb {P} ({\ mathcal {E}}) \ = \ \ lim _ {n} \ mathbb {P} (Z_ {n} = 0).}

Además la continuación

{\ Displaystyle u_ {n} \ = \ \ mathbb {P} (Z_ {n} = 0)}

está definido por (char ), y por la relación de recurrencia ${\ Displaystyle u_ {0} = 0}$ ${\ Displaystyle Z_ {0} = 1}$

{\ Displaystyle u_ {n + 1} \ = \ \ varphi (u_ {n}),}

lo que lleva a ver como un punto fijo de φ . ${\ Displaystyle \ mathbb {P} ({\ mathcal {E}})}$

Para probar la relación de recurrencia en , observemos que ${\ Displaystyle u_ {n},}$

{\ Displaystyle \ varphi _ {n} (0) \ = \ \ mathbb {P} (Z_ {n} = 0) \ = \ u_ {n}.}

Entonces

{\ Displaystyle u_ {n + 1} \ = \ \ varphi _ {n + 1} (0) \ = \ \ varphi (\ varphi _ {n} (0)) \ = \ \ varphi (u_ {n}) .}

Ahora, suponga que hay un punto fijo de en el intervalo [0,1] . Entonces, siendo la función creciente en el intervalo [0,1] , entra entonces, por inducción, Pero, por un lado, (que se puede reescribir ), por otro lado Así, la secuencia es creciente y aumentada en 1, por lo tanto convergente. Además, hemos visto que la secuencia está limitada por cualquier punto fijo de pertenencia al intervalo [0,1] . Por tanto, el límite de la secuencia también se incrementa en cualquier punto fijo de pertenencia al intervalo [0,1] . Pero como la función es continua en el intervalo [0,1] , su límite es uno de los puntos fijos de la función y por tanto, necesariamente, el más pequeño de ellos. $\Ana$ $\ varphi$ $\ varphi$ ${\ Displaystyle \ {u_ {0} \ leq \ ell \ {\ text {y}} \ u_ {0} \ leq u_ {1} \}}$ ${\ Displaystyle \ {u_ {0} \ leq u_ {1} \ leq \ ell \},}$ ${\ Displaystyle \ {\ forall n, \ u_ {n} \ leq u_ {n + 1} \ leq \ ell \}.}$ ${\ Displaystyle \ varphi (0) = p_ {0} \ geq 0}$ ${\ Displaystyle u_ {1} \ geq u_ {0}}$ ${\ Displaystyle \ varphi (1) = 1.}$ ${\ Displaystyle (u_ {n}) _ {n \ geq 0}}$ ${\ Displaystyle (u_ {n}) _ {n \ geq 0}}$ $\Ana$ $\ varphi$ ${\ Displaystyle (u_ {n}) _ {n \ geq 0}}$ $\Ana$ $\ varphi$ $\ varphi$ $\ varphi,$

Como es toda una serie de radio de convergencia al menos igual a 1, con coeficientes positivos o cero, es convexa (e incluso estrictamente convexa si p 0 + p 1 <1 ), e indefinidamente diferenciable en el intervalo ] 0.1 [ , y por lo tanto tiene como máximo 2 puntos fijos en el intervalo [0,1] , a menos que en 2007 se haya probado un teorema análogo sobre mapas planos aleatorios (una generalización natural de árboles aleatorios). $\ varphi$ $\ varphi$ ${\ Displaystyle \ varphi (s) \ equiv s.}$

Ejemplo:

si el teorema dice que la probabilidad de extinción es cero. Esto se puede ver directamente sin dificultad, porque equivale a lo que implica inmediatamente que cada generación esté formada exactamente por un individuo; ${\ Displaystyle \ varphi (s) \ equiv s,}$ ${\ Displaystyle \ mathbb {P} ({\ mathcal {E}})}$ ${\ Displaystyle \ varphi (s) \ equiv s}$ ${\ Displaystyle p_ {1} = 1,}$
más en general, si 0 es un punto fijo , entonces, según el teorema, es cero (podríamos verlo directamente, ya que, en este caso, cada individuo de la población tiene al menos un hijo); ${\ Displaystyle p_ {0} = 0,}$ ${\ Displaystyle \ mathbb {P} ({\ mathcal {E}})}$
si los dos puntos fijos son 1 y entonces, como era de esperar, la probabilidad de extinción es 1 si y es menor que 1 (de hecho ) si Aquí, el valor de es difícil de calcular directamente, sin usar el teorema. La figura de al lado muestra varios valores de y la correspondiente probabilidad de extinción. ${\ Displaystyle p_ {0} + p_ {2} = 1,}$ ${\ Displaystyle p_ {0} / p_ {2},}$ ${\ Displaystyle p_ {0} \ geq p_ {2},}$ ${\ Displaystyle \ mathbb {P} ({\ mathcal {E}}) = p_ {0} / p_ {2}}$ ${\ Displaystyle p_ {0} <p_ {2}.}$ ${\ Displaystyle \ mathbb {P} ({\ mathcal {E}})}$ ${\ Displaystyle p_ {0},}$

Más generalmente

Teorema : hay 3 casos:

Caso subíndice ( m <1 ). La probabilidad de extinción es 1. ${\ Displaystyle \ mathbb {P} ({\ mathcal {E}})}$
Caso crítico ( m = 1 ). La probabilidad de extinción es igual a 1, a menos que y, en este último caso, la probabilidad de extinción sea cero. ${\ Displaystyle \ mathbb {P} ({\ mathcal {E}})}$ ${\ Displaystyle p_ {1} = 1,}$
Caso supercrítico ( m> 1 ). La probabilidad de extinción es estrictamente menor que 1 (y es el punto fijo más pequeño de φ en el intervalo [0,1] ). ${\ Displaystyle \ mathbb {P} ({\ mathcal {E}})}$

Demostración

Esto resulta de lo que

{\ Displaystyle m \ = \ \ varphi ^ {\ prime} (1).}

En efecto :

Caso crítico . Si m <1 , la tangente en (1,1) a la gráfica de φ está, en el intervalo [0,1 [ , estrictamente por encima de la línea de ecuación y = x , y, siendo φ convexa, la gráfica de φ es por encima de su tangente, por lo tanto, también, estrictamente por encima de la línea de ecuación y = x : el único punto fijo de φ es 1.
Caso crítico . Si m = 1 , la tangente en (1,1) a la gráfica de φ es la recta de la ecuación y = x . Si φ es estrictamente convexo, la gráfica de φ está estrictamente por encima de su tangente, por lo que el único punto fijo de φ es 1. Ahora φ es estrictamente convexo si y solo si (como vemos al calcular la segunda derivada de φ ). De lo contrario, φ es una función afín , por lo que su gráfica se confunde con sus tangentes, en particular, aquí, con la recta de la ecuación y = x . Entonces ${\ Displaystyle p_ {0} + p_ {1} <1}$ ${\ Displaystyle p_ {1} = 1.}$
Caso supercrítico . Si m> 1 , la tangente en (1,1) a la gráfica de φ está estrictamente debajo de la línea de ecuación y = x , por lo tanto, en un intervalo [1-ε, 1 [ bien elegido, φ him- mismo es estrictamente debajo de la recta de la ecuación y = x . En 0, por otro lado, ya que la gráfica de φ está por encima de la línea de la ecuación y = x . Entonces, en virtud del teorema del valor intermedio , φ tiene un punto fijo estrictamente menor que 1. ${\ Displaystyle \ varphi (0) = p_ {0} \ geq 0,}$

El comportamiento del proceso de Galton-Watson en los casos subíndices y supercríticos corresponde a la intuición. Por otro lado, el comportamiento del proceso de Galton-Watson en el caso crítico aleatorio (la extinción es cierta) es radicalmente diferente del comportamiento del proceso de Galton-Watson en el caso crítico determinista (cada individuo tiene exactamente un hijo y el la extinción es imposible).

También para ver

Notas

" Tres artículos sobre la historia de los procesos de ramificación " , en stat.washington.edu (consultado el 23 de marzo de 2018 )
Jacques Neveu , " Árboles y procesos de Galton-Watson ", Ann. del PHI , vol. 22, n o 21986( leer en línea ) (sección 2)
(en) H. Kesten y BP Stigum , " Un teorema del límite para los procesos multidimensionales de Galton-Watson " , The Annals of Mathematical Statistics , vol. 37, n o 5,Octubre de 1966, p. 1211-1223 ( leer en línea )
(in) Krishna B. Athreya , " Una prueba simple de un resultado de Kesten y Stigum en el proceso de ramificación de Galton-Watson multitipo supercrítico " , The Annals of Mathematical Statistics , vol. 41, n o 1,Febrero de 1970, p. 195-202 ( leer en línea )
(en) Jean-François Marckert y Gregory Miermont , " Principios de invariancia para mapas planos bipartitos aleatorios " , Ann. Probab. , vol. 35, n o 5,2007, p. 1642-1705 ( DOI 10.1214 / 009117906000000908 , leer en línea ), Proposición 1.

Bibliografía

(en) Krishna B. Athreya y Peter E. Ney , Procesos de ramificación , Publicaciones de Dover ,19 de marzo de 2004, 2 nd ed. , 304 p. ( ISBN 978-0-486-43474-2 , leer en línea )
(en) Theodore E. Harris , La teoría de los procesos de ramificación , Publicaciones de Dover ,Mayo de 2002, 2 nd ed. , 256 p. ( ISBN 978-0-486-49508-8 )
Artículo original de Galton y Watson: Sobre la probabilidad de extinción de familias
Tesis en línea sobre dinámica de poblaciones que explica en el capítulo 1 el modelo de Galton-Watson

Enlaces útiles