Diagrama de Hasse
En matemáticas , el diagrama de Hasse , que lleva el nombre del matemático alemán Helmut Hasse , es una representación visual de un orden finito. Similar a la representación habitual de un gráfico en papel, facilita su comprensión.
En un diagrama de Hasse:
- Los elementos ordenados están representados por puntos.
- La relación entre dos elementos está representada por un segmento entre dos puntos.
- Si un elemento x es ≤ a otro elemento y , entonces el punto que representa x se coloca más bajo que el de y . Por lo tanto, no es necesario señalar con flechas los segmentos para que se describa su orientación.
- Para evitar sobrecargar el diagrama, las posibles relaciones de orden no están todas representadas. Se limitan a la reducción reflexiva transitiva:
- Cuando x <y , si existe z tal que x <z <y , entonces ningún segmento debe vincular x con y .
- No se muestran los bucles de un elemento a sí mismo.
- Cuidamos al máximo de no cruzar los segmentos.
Tenga en cuenta que en el caso de un orden infinito, todavía podemos usar el diagrama de Hasse y representar una restricción finita del orden.
Ejemplos de diagramas de Hasse
- Un conjunto ordenado de once elementos cuyos tres máximos son los tres límites superiores y el elemento mínimo es tanto el límite inferior único como el límite inferior del conjunto.

- Pour l'ensemble des diviseurs de 60, A = {1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60}, ordonnés par la relation de divisibilité, on obtient le diagramme de Hasse Próximo :

- El conjunto S = A ∪ B ∪ C ∪ D, donde A, B, C y D son cuatrillizos de booleanos que representan las posibles combinaciones de las partes de S, de manera que,
B = { 0100 = {b}, 1100 = {a, b}, 0110 = {b, c}, 0101 = {b, d}, 1110 = {a, b, c}, 1101 = {a, b, d}, 0111 = {b, c, d}, 1111 = {a, b, c, d}}
C = { 0010 = {c}, 1010 = {a, c}, 0110 = {b, c}, 0011 = {c, d}, 1110 = {a, b, c}, 1011 = {a, c, d}, 0111 = {b, c, d}, 1111 = {a, b, c, d}}
D = { 0001 = {d}, 1001 = {a, d}, 0101 = {b, d}, 0011 = {c, d}, 1101 = {a, b, d}, 1011 = {a, c, d}, 0111 = {b, c, d}, 1111 = {a, b, c, d}} S = { 0000 = {}, 1000 = {a}, 0100 = {b}, 0010 = {c}, 0001 = {d}, 1100 = {a, b}, 1010 = {a, c}, 1001 = {a, d}, 0110 = {b, c}, 0101 = {b, d}, 0011 = {c, d}, 1110 = {a, b, c}, 1101 = {a, b, d}, 1011 = {a, c, d}, 0111 = {b, c, d}, 1111 = {a, b, c, d}}
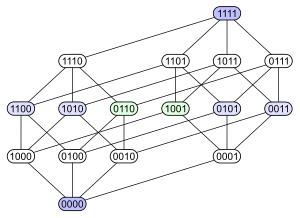
Así, de los dieciséis cuatrillizos ordenados por la relación de inclusión, obtenemos el siguiente diagrama de Hasse:
 |
 |
 |

|
Todas estas cuatro figuras representan el mismo diagrama de Hasse pero bajo diferentes aspectos para demostrar diferentes propiedades:
- El primer diagrama ilustra el hecho de que el conjunto de partes (de S ) es un conjunto graduado parcialmente ordenado: el rango de cada elemento (parte de S ) corresponde a su altura en el diagrama;
- El segundo diagrama también respeta esta correspondencia entre fila y altura, pero le agrega al estirar ciertos bordes una mejora del tesseract como una unión de dos cubos (al interpretar los cuatrillizos booleanos como coordenadas en la dimensión 4, cada una correspondiente entonces a una parte superior de el hipercubo);
- El tercer diagrama enfatiza la simetría interna de la estructura;
- El cuarto diagrama muestra vértices dispuestos de manera análoga a los coeficientes de una matriz cuadrada de orden 4.