Teorema de Cantor-Bernstein

El teorema de Cantor-Bernstein , también conocido como teorema de Cantor-Schröder-Bernstein , es el teorema de la teoría de conjuntos que establece la existencia de una biyección entre dos conjuntos cuando hay dos inyecciones , una de la segunda a la primera y la otra de la primera a la segundo.

Teorema : si hay una inyección de un conjunto E a un conjunto F y una inyección de F a E, entonces hay una biyección de E a F.

Lleva el nombre de los matemáticos Georg Cantor , Felix Bernstein y Ernst Schröder . Cantor dio una primera demostración de esto, pero que usó implícitamente el axioma de elección . Bernstein dio una demostración que no dependía de este axioma. Sin embargo, todas las demostraciones dadas utilizan el principio del tercero excluido y, por tanto, no son aceptadas por los intuicionistas .

Histórico

Georg Cantor declaró este teorema sin demostración en 1887. En 1895, Cantor comentó en la primera parte de Beiträge zur Begründung der transfiniten Mengenlehre ("Sobre los fundamentos de la teoría de conjuntos transfinitos") que el teorema se deduce de la propiedad de tricotomía para el cardinales (Cantor de hecho considera que cualquier conjunto puede estar bien ordenado , lo que equivale al axioma de elección ), pero pospone la prueba de esta propiedad para una publicación posterior.

Felix Bernstein , un alumno de éste, produjo una demostración que no utilizó los órdenes correctos (y no requirió el axioma de la elección) ya en 1896 a la edad de 18 años. Fue publicado en 1898 a propuesta de Cantor en Lecciones sobre la teoría de funciones bajo la pluma de Émile Borel .

Ernst Schröder también publicó una demostración en 1898, pero resultó estar equivocada. El error fue detectado en 1902 por Alwin Korselt, quien informó a Schröder desde el principio.Mayo de 1902. Este último reconoce que la autoría de la demostración del teorema recae íntegramente en Bernstein, en una respuesta enviada quince días después (un mes antes de su muerte). Añade que él mismo se dio cuenta del problema en 1901 y se lo contó a su amigo Max Dehn .

Korselt se somete al final Mayo de 1902un artículo en el Mathematische Annalen , donde expone el error de Schröder y propone otra prueba, pero esta no se publica hasta 1911. Durante este tiempo la prueba de Schröder es considerada correcta, en particular por Cantor, Peano y Schönflies .

Richard Dedekind había escrito una prueba del teorema de Cantor-Bernstein ya en 1887, para lo cual utilizó su teoría de las cadenas publicada en su obra Was sind und was sollen die Zahlen? (1888). Fue encontrado después de su muerte y publicado solo en 1930 .

Entonces, ignorando esta prueba, Ernst Zermelo publicó dos pruebas del teorema en 1901 y luego en 1908, ambas basadas en la teoría de la cadena de Dedekind, la segunda de las cuales resulta ser muy similar a la de Dedekind. Zermelo ya había enviado su segunda demostración a Poincaré a principios de 1906 , en respuesta a una crítica de Poincaré sobre el uso de la inducción completa ( definición por inducción y razonamiento por inducción ) en las entonces conocidas demostraciones del teorema de Cantor-Bernstein. Esta revisión va acompañada de una versión detallada de la prueba de Bernstein-Borel que destaca el uso de la inducción completa. Había sido publicado en la Revue de métaphysique et de morale enEnero 1906. La prueba de Zermelo no usa números enteros y, por lo tanto, obviamente no tiene recurrencia. En respuesta, Poincaré publicó en la misma revista en mayo del mismo año una adaptación en francés de la manifestación de Zermelo, de la que criticó el uso de la imprevisibilidad , críticas a las que Zermelo respondió en 1908.

Tres demostraciones

Primera demostración

Lema preliminar

Comenzamos mostrando que si es un mapa inyectivo de un conjunto a una de sus partes , entonces existe una biyección desde el principio . $tu$ $A$ $B$ $v$ $A$ $B$

Dejemos que la secuencia se defina por: ${\ Displaystyle (C_ {n}) _ {n \ in \ mathbb {N}}}$

{\ Displaystyle \ left \ {{\ begin {matrix} C_ {0} = A \ setminus B \\\ forll n \ in \ mathbb {N} ^ {*}, C_ {n} = u (C_ {n- 1}) \ end {matriz}} \ right.}

Es la reunión de todos los conjuntos : . $VS$ ${\ Displaystyle (C_ {n}) _ {n \ in \ mathbb {N}}}$ ${\ Displaystyle C = \ bigcup _ {n \ in \ mathbb {N}} C_ {n}}$

Sea entonces la aplicación de in definida por: $v$ $A$ $B$

{\ begin {matriz} v: & x \ en C & \ mapsto & u (x) \\ & x \ notin C & \ mapsto & x \ end {matriz}}

$v$ está bien definido con valores en , porque está con valores en , y si entonces y así . $B$ $tu$ $B$ $x \ notin C$ ${\ Displaystyle x \ notin C_ {0}}$ $x \ en B$

$v$ injectively envía en ; y el complementario de idénticamente en sí mismo. Entonces es una inyección. $VS$ $u (C) = \ cup _ {{n \ in \ mathbb {N}}} u (C_ {n}) = \ cup _ {{m \ in \ mathbb {N} ^ {*}}} C_ {m } \ subconjunto C$ $VS$

Demostremos que es sobreyectiva. O bien . Demostremos que existe tal que . $v$ ${\ Displaystyle y \ in B}$ $x \ en A$ $v (x) = y$

Si : entonces existe tal que ( es estrictamente positivo porque , por tanto ). Por tanto , existe tal que . $y \ en C$ ${\ Displaystyle i \ in \ mathbb {N} ^ {*}}$ ${\ Displaystyle y \ en C_ {i}}$ $I$ ${\ Displaystyle y \ in B}$ ${\ Displaystyle y \ notin C_ {0}}$ ${\ Displaystyle x \ in C_ {i-1} \ subconjunto C}$ $v (x) = u (x) = y$
Si : entonces ${\ Displaystyle y \ notin C}$ $v (y) = y$

Por tanto, es biyectiva, lo que prueba la primera proposición. $v$

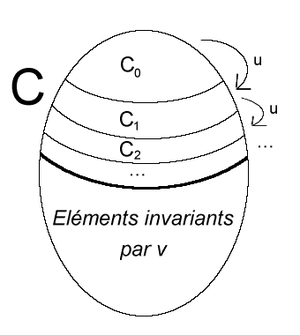
Interpretación

Podemos dar una interpretación del resultado mostrado arriba. A es el conjunto (infinito) de espectadores en un teatro (infinito). Cada espectador tiene reservado un lugar, e inicialmente se asume que cada lugar está ocupado por un espectador, pero no necesariamente por el espectador que reservó ese lugar. B es entonces el conjunto de espectadores sentados. Además, al ser los decorados infinitos, es posible seguir siendo espectadores de pie. La aplicación u es la aplicación que asocia, con un espectador x , el espectador y = u ( x ) sentado en lugar de x .

$C_ {0}$ es el conjunto de espectadores inicialmente de pie. Estos espectadores van a sus asientos y desalojan a los ocupantes. Estos luego forman el todo . Ellos hacen lo mismo. designa los espectadores de pie en el n esima etapa. Van a los lugares que tienen reservados y expulsan a sus ocupantes. Repetimos un número infinito de veces. C designa a todos los espectadores que se han puesto de pie al menos una vez (incluidos los que estaban de pie inicialmente). $C_1$ $C_ {n}$

La aplicación v designa la aplicación que asocia, con un espectador x que debe ponerse de pie, al espectador y que va a desalojar, o bien que, con un espectador x que permanece siempre sentado, se asocia x él mismo. La aplicación recíproca de v es la aplicación que, para un espectador y perturbado, asocia al espectador x que viene a ocupar su lugar, o que se asocia, con un espectador y nunca perturbado, y él mismo.

Prueba final del teorema

Entonces mostremos el teorema inicial.

Sea B = g ( F ) la imagen de F por inyección g . El mapa u = g o f es una inyección de E en B , con . Así que hay una biyección v de E sobre B . Como g es una inyección y g ( F ) = B , define una biyección restricción h de F en B . El compuesto h -1 ∘ v es una biyección de E a F , lo que demuestra el teorema de Cantor-Bernstein. $B \ subconjunto E$

Segunda demostración

Un lema preliminar

Esta demostración se basa en el siguiente lema, un caso particular del teorema de Knaster-Tarski .

Sea un conjunto, el conjunto de sus partes y una aplicación creciente, es decir tal que . Entonces admite un punto fijo , es decir, existe una parte de tal que . $mi$ $EDUCACIÓN FÍSICA)$ ${\ Displaystyle G: P (E) \ a P (E)}$ ${\ Displaystyle A \ subconjunto B \ Rightarrow G (A) \ subconjunto G (B)}$ $GRAMO$ $METRO$ $mi$ $G (M) = M$

Demostración final

Ahora inyectemos in e inyectemos in . Pour toute partie de , on pose , c'est-à-dire que s'obtient en prenant l' image directe , puis le complémentaire dans de cette image, puis l'image directe par de ce complémentaire, et enfin le complémentaire dans de esta imagen. No es difícil comprobar que está aumentando. $F$ $mi$ $F$ $gramo$ $F$ $mi$ $A$ $mi$ ${\ Displaystyle G (A) = E \ setminus g \ left [F \ setminus f (A) \ right]}$ ${\ Displaystyle G (A)}$ ${\ Displaystyle f (A)}$ $F$ $gramo$ $mi$ ${\ Displaystyle G: P (E) \ a P (E)}$

Luego presentamos la parte del lema preliminar. Esta parte es invariante en , lo que significa que es el complemento de en . $METRO$ $GRAMO$ ${\ Displaystyle g \ left [F \ setminus f (M) \ right]}$ $METRO$ $mi$

Definimos una biyección planteando: ${\ Displaystyle h: E \ a F}$

si ;

x \ en M, h (x) = f (x)

si .

x \ notin M, h (x) = g ^ {{- 1}} (x)

$METRO$ juega un papel comparable al de la primera demostración o al de la siguiente demostración. $VS$ ${\ Displaystyle E_ {E} \ cup E _ {\ infty}}$

Tercera demostración

Esta demostración es esencialmente la publicada por Julius König en 1906, y a menudo se repite desde entonces.

Supongamos, sin pérdida de generalidad , que y son inconexos . $mi$ $F$

Al elemento de , asociamos una secuencia finita o infinita definida por inducción de la siguiente manera. El valor inicial es . Supongamos que está definido (de lo contrario, no definido), entonces: $X$ $mi$ ${\ Displaystyle (x_ {0}, x_ {1}, \ dots)}$ ${\ Displaystyle x_ {0} = x}$ $x_ {n}$ $x _ {{n + 1}}$

si tiene un antecedente por g , entonces este antecedente (único) (nota: en este caso n es par); ${\ Displaystyle x_ {n} \ in E}$ $x _ {{n + 1}}$
si está definido y tiene un antecedente por f , entonces es este antecedente (único) (nota: en este caso n es impar); $x_ {n}$ ${\ Displaystyle x_ {n} \ in F}$ $x _ {{n + 1}}$
en los demás casos no está definido. $x _ {{n + 1}}$

Entonces son posibles tres casos para la continuación que hacen posible la partición en tres conjuntos: ${\ Displaystyle (x_ {0}, x_ {1}, \ dots)}$ $mi$

${\ Displaystyle E_ {E}}$ es el conjunto de tal que la secuencia correspondiente es finita y se detiene en un elemento de (de manera equivalente, el índice del último elemento es par); $x \ en E$ ${\ Displaystyle (x_ {0}, x_ {1}, \ dots)}$ $mi$
$E_F$ es el conjunto de tal que la secuencia correspondiente es finita y se detiene en un elemento de (de manera equivalente, el índice del último elemento es impar); $x \ en E$ ${\ Displaystyle (x_ {0}, x_ {1}, \ dots)}$ $F$
$E_ \ infty$ es el conjunto de tal que la secuencia correspondiente es infinita. $x \ en E$ ${\ Displaystyle (x_ {0}, x_ {1}, \ dots)}$

Particionamos de forma similar en , y . Entonces : $F$ ${\ Displaystyle F_ {F}}$ ${\ Displaystyle F_ {E}}$ $F _ {\ infty}$

$F$ es una biyección de on , así como de on ; ${\ Displaystyle E_ {E}}$ ${\ Displaystyle F_ {E}}$ $E_ \ infty$ $F _ {\ infty}$
$gramo$ es una biyección de sobre , y por lo tanto su recíproco es una biyección de sobre . ${\ Displaystyle F_ {F}}$ $E_F$ $E_F$ ${\ Displaystyle F_ {F}}$

Obtenemos así una biyección de on . $mi$ $F$

Generalización

Deje X un conjunto no vacío y una relación de equivalencia en el conjunto de subconjuntos de X . Suponemos que satisface las dos propiedades: $\ sim$

si existe una biyección tal que, para cualquier parte de , ; ${\ Displaystyle A \ sim B}$ $f: A \ a B$ $VS$ $A$ ${\ Displaystyle f (C) \ sim C}$
si y y luego . ${\ Displaystyle A_ {1} \ cap A_ {2} = B_ {1} \ cap B_ {2} = \ varnothing}$ ${\ Displaystyle A_ {1} \ sim B_ {1}}$ ${\ Displaystyle A_ {2} \ sim B_ {2}}$ ${\ Displaystyle A_ {1} \ cup A_ {2} \ sim B_ {1} \ cup B_ {2}}$

Sean dos conjuntos y , un subconjunto de y un subconjunto de . Asumimos eso y . Entonces . $A$ $B$ $A_1$ $A$ $B_1$ $B$ ${\ Displaystyle A \ sim B_ {1}}$ ${\ Displaystyle B \ sim A_ {1}}$ ${\ Displaystyle A \ sim B}$

Esta generalización también se puede demostrar sin el axioma de elección .

En el caso particular donde y es la relación de equipotencia , encontramos el resultado anterior. ${\ Displaystyle X = E \ cup F}$ $\ sim$

Notas y referencias

(in) Ettore Carruccio, Matemáticas y lógica en la historia y en el pensamiento contemporáneo , Transaction Publishers,2006( ISBN 978-0-202-30850-0 ) , pág. 354
Georg Cantor, Sobre los fundamentos de la teoría de conjuntos transfinitos , trad. Francés de 1899, declaración p. 347
demostración p. 395, en Gallica.
F. Casiro, “El teorema de Cantor-Bernstein”, Tangente , mayo-junio de 2008, p. 42-44.
Émile Borel, Lecciones sobre la teoría de funciones , p. 104 .
(de) Ernst Schröder , " Ueber zwei Definitionen der Endlichkeit und G. Cantor'sche Sätze " , Johann Ambrosius Barth Verlag , Halle a. S., Kaiserliche Leopoldino-Carolinische Deutsche Akademie der Naturforscher, vol. 71, n o 6,1898, p. 303-362 (336-344) ( leer en línea ).
" ... la pregunta de por qué el nombre de Schröder se asocia tan a menudo con un resultado hacia el cual su única contribución fue proporcionar una prueba falaz. " , (En) William W. Tait (en) , " Michael Potter, Teoría de conjuntos y su filosofía (Reseña del libro) " , Historia y filosofía de la lógica , vol. 26, n o 22005, p. 162-166 ( leer en línea ), p. 164 .
(de) Alwin Korselt , " Über einen Beweis des Äquivalenzsatzes " , B. G. Teubner , Leipzig, vol. 70, n o 21911, p. 294–296 ( ISSN 0025-5831 , DOI 10.1007 / bf01461161 , leer en línea )
" … Daß ich Herrn F. Bernstein die Ehre, den G. Cantorschen Satz bewiesen zu haben, allein überlasse, hatte ich einstweilen einem Freunde desselben, Herrn Dr. Max Dehn (jetzt en Münster) schon vorigen Herbst resp. Sommer - natürlich zum Weitergeben - gesagt ” , extracto de una carta de Schröder a Körselt del 23 de mayo de 1902, citada por Korselt 1911 .
(en) Gregory H. Moore , El axioma de elección de Zermelo Sus orígenes, desarrollo e influencia Springer al. "Estudios de Historia de las Matemáticas y Ciencias Físicas" ( n o 8),mil novecientos ochenta y dos( ISBN 978-0-387-90670-6 ) , pág. 48.
Hinkis , 2013 , p. 87.
Hinkis , 2013 , p. 89.
Hinkis , 2013 , p. 129.
Hinkis , 2013 , p. 196.
J. König, " Sobre la teoría de conjuntos ", Informes semanales de las sesiones de la Academia de Ciencias , vol. 143,1906, p. 110-112 ( leer en línea ).
Por ejemplo, Garrett Birkhoff y Saunders Mac Lane , A Survey of Modern Algebra , Macmillan ,1977( 1 st ed. 1941) ( ISBN 0-02-310070-2 ) , p. 387-388, Andreï Kolmogorov y Sergei Fomin , Elementos de la teoría de funciones y análisis funcional , Mir,1977, p. 22(primera edición en francés 1974), (en) John L.Kelley , General Topology , Van Nostrand,1955( leer en línea ) , pág. 28(reeditado por Springer-Verlag), René Cori y Daniel Lascar , Lógica matemática II . Funciones recursivas, teorema de Gödel, teoría de conjuntos, teoría de modelos [ detalle de ediciones ]1993.
Esta demostración sigue de cerca a Kolmogorov y Fomine 1977 , p. 22 y Cori y Lascar 1993 , p. 148-149, que simplifican ligeramente a König 1906 y explican el uso de la definición por inducción, y por tanto de enteros. La prueba de Kelley 1955 que no hace explícita la definición de las secuencias recurrentes es incorrecta, porque la partición se define según el carácter finito y la paridad del número de elementos del conjunto de imágenes de las secuencias y . Ahora bien, este conjunto puede ser finito, si la secuencia correspondiente es infinita pero tiene un ciclo. Esto fue notado por Leslie Lamport , How to Write a Proof , 1993, p. 8, quien toma esta prueba como ejemplo de una falsa prueba informal, cuyo error aparece cuando intenta presentarla de forma estructurada, pero que por lo demás es difícil de detectar. $(x_ {n})$ $(y_ {n})$
(en) Stan Wagon , La paradoja de Banach-Tarski , UPC ,1993, 253 p. ( ISBN 978-0-521-45704-0 , leer en línea ) .

Ver también

Bibliografía

(en) Marcel Crabbé, “ Teorema de Cantor-Bernstein en un Semiring ” , The Mathematical Intelligencer , vol. 33, n o 3,2011, p. 80 ( leer en línea )
(en) Arie Hinkis , Demostraciones del teorema de Cantor-Bernstein, una excursión matemática , Birkhäuser,2013, 456 p. ( ISBN 978-3-0348-0788-3 , DOI 10.1007 / 978-3-0348-0224-6 )