Ley Zeta
En teoría de probabilidad y estadística , la distribución zeta es un escenario de acto discreto .
s>1{\ Displaystyle s> 1}
Definición
Decimos que una variable aleatoria sigue una ley zeta de parámetros si:
X{\ Displaystyle X}
s{\ Displaystyle s}
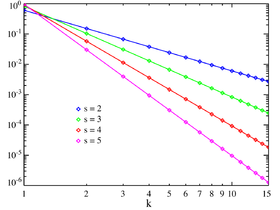
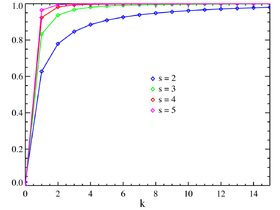
PAG(X=k)=k-s/ζ(s){\ Displaystyle \ mathbb {P} (X = k) = k ^ {- s} / \ zeta (s) \,}
donde la función zeta de Riemann no está definida en 1.
ζ{\ Displaystyle \ zeta}
Momentos
El n-ésimo momento está definido por la expectativa de X n :
metrono=mi(Xno)=1ζ(s)∑k=1∞1ks-no{\ Displaystyle m_ {n} = \ mathbb {E} (X ^ {n}) = {\ frac {1} {\ zeta (s)}} \ sum _ {k = 1} ^ {\ infty} {\ frac {1} {k ^ {sn}}}}
La serie de la derecha es una representación de la función zeta de Riemann y converge solo para valores de sn estrictamente mayores que 1. Por lo tanto:
metrono={ζ(s-no)/ζ(s)para no<s-1∞para no≥s-1{\ Displaystyle m_ {n} = \ left \ {{\ begin {matrix} \ zeta (sn) / \ zeta (s) & {\ textrm {for}} ~ n <s-1 \\\ infty & {\ textrm {verter}} ~ n \ geq s-1 \ end {matriz}} \ right.}
Vínculo con la densidad natural
Sea A parte de , decimos que A tiene una densidad natural si converge. Denote por d (A) el límite. Entonces tenemos el siguiente resultado:NO{\ Displaystyle \ mathbb {N}}
Tarjeta(A∩{1,...,no})no{\ displaystyle {\ frac {\ operatorname {Card} (A \ cap \ {1, \ dots, n \})} {n}}}
PAGs(X∈A)⟶s→1+D(A){\ Displaystyle \ mathbb {P} _ {s} (X \ in A) {\ underset {s \ rightarrow 1 ^ {+}} {\ longrightarrow}} d (A)}
Demostración
O bien , supongamos para todo lo
que tenemos por hipótesis que , por lo tanto, podemos plantear como
Entonces escribimos
Estamos interesados en el término , tenemos: porque la variable ficticia a es mayor que
Sin dañar la generalidad, supongamos A infinito (el caso Un acabado es trivial), luego escribe . De ello se deduce entonces que para . entonces establezcamos
We por lo tanto , por
lo tanto Hacemos lo mismo a la izquierda y encontramos para s lo suficientemente cerca de 1 que , así:ϵ>0{\ Displaystyle \ epsilon> 0}
no∈NO,vsno=Tarjeta(A∩{1,...,no}){\ Displaystyle n \ in \ mathbb {N}, c_ {n} = \ operatorname {Card} (A \ cap \ {1, \ dots, n \})}
limno→∞vsnono=D(A){\ Displaystyle \ lim _ {n \ to \ infty} {\ frac {c_ {n}} {n}} = d (A)}
no0∈NO{\ Displaystyle n_ {0} \ in \ mathbb {N}}
∀no∈NO,no≥no0⇒|vsnono-D(A)|≤ϵ.{\ Displaystyle \ forall n \ in \ mathbb {N}, n \ geq n_ {0} \ Rightarrow | {\ frac {c_ {n}} {n}} - d (A) | \ leq \ epsilon.}
PAGs(X∈A)=∑a∈A1asζ(s)=∑a∈Aa<no01as+∑a∈Aa≥no01asζ(s){\ Displaystyle \ mathbb {P} _ {s} (X \ in A) = {\ frac {\ sum _ {a \ in A} {\ frac {1} {a ^ {s}}}} {\ zeta (s)}} = {\ frac {\ sum _ {\ underset {a <n_ {0}} {a \ in A}} {\ frac {1} {a ^ {s}}} + \ sum _ { \ underset {a \ geq n_ {0}} {a \ in A}} {\ frac {1} {a ^ {s}}}} {\ zeta (s)}}}
∑a∈Aa≥no01as{\ Displaystyle \ sum _ {\ underset {a \ geq n_ {0}} {a \ in A}} {\ frac {1} {a ^ {s}}}}
∑a∈Aa≥no01as=∑a∈Aa≥no0vsasvsasas≤∑a∈Aa≥no0(D(A)+ϵ)svsas{\ Displaystyle \ sum _ {\ underset {a \ geq n_ {0}} {a \ in A}} {\ frac {1} {a ^ {s}}} = \ sum _ {\ underset {a \ geq n_ {0}} {a \ in A}} {\ frac {c_ {a} ^ {s}} {c_ {a} ^ {s} a ^ {s}}} \ leq \ sum _ {\ underset { a \ geq n_ {0}} {a \ in A}} {\ frac {(d (A) + \ epsilon) ^ {s}} {c_ {a} ^ {s}}}}
no0.{\ Displaystyle n_ {0}.}
A={a0,a1,...}{\ Displaystyle A = \ {a_ {0}, a_ {1}, \ dots \}}
metro∈NO,vsametro=metro{\ Displaystyle m \ in \ mathbb {N}, c_ {a_ {m}} = m}
no1=min({metro∈NO,ametro≥no0}).{\ Displaystyle n_ {1} = \ operatorname {min} (\ {m \ in \ mathbb {N}, a_ {m} \ geq n_ {0} \}).}
∑a∈Aa≥no01vsasζ(s)=∑metro=1∞1metros-∑metro=1no1-11metrosζ(s)=ζ(s)-∑metro=1no1-11metrosζ(s)=1-∑metro=1no1-11metrosζ(s)⟶s→1+1{\ Displaystyle {\ frac {\ sum _ {\ underset {a \ geq n_ {0}} {a \ in A}} {\ frac {1} {c_ {a} ^ {s}}}} {\ zeta (s)}} = {\ frac {\ sum _ {m = 1} ^ {\ infty} {\ frac {1} {m ^ {s}}} - \ sum _ {m = 1} ^ {n_ { 1} -1} {\ frac {1} {m ^ {s}}}} {\ zeta (s)}} = {\ frac {\ zeta (s) - \ sum _ {m = 1} ^ {n_ {1} -1} {\ frac {1} {m ^ {s}}}} {\ zeta (s)}} = 1 - {\ frac {\ sum _ {m = 1} ^ {n_ {1} -1} {\ frac {1} {m ^ {s}}}} {\ zeta (s)}} {\ underset {s \ rightarrow 1 ^ {+}} {\ longrightarrow}} 1}
PAGs(X∈A)≤∑a∈Aa<no01asζ(s)+(D(A)+ϵ)s(1-∑metro=1no1-11metrosζ(s))⟶s→1+D(A)+ϵ{\ Displaystyle \ mathbb {P} _ {s} (X \ in A) \ leq {\ frac {\ sum _ {\ underset {a <n_ {0}} {a \ in A}} {\ frac {1 } {a ^ {s}}}} {\ zeta (s)}} + (d (A) + \ epsilon) ^ {s} (1 - {\ frac {\ sum _ {m = 1} ^ {n_ {1} -1} {\ frac {1} {m ^ {s}}}} {\ zeta (s)}}) {\ underset {s \ rightarrow 1 ^ {+}} {\ longrightarrow}} d ( A) + \ epsilon}
D(A)-2ϵ≤PAGs(X∈A)≤D(A)+2ϵ{\ Displaystyle d (A) -2 \ epsilon \ leq \ mathbb {P} _ {s} (X \ in A) \ leq d (A) +2 \ epsilon}
PAGs(X∈A)⟶s→1+D(A){\ Displaystyle \ mathbb {P} _ {s} (X \ in A) {\ underset {s \ rightarrow 1 ^ {+}} {\ longrightarrow}} d (A)}
Ver también
Referencias
