Simplex

En matemáticas , y más particularmente en geometría , un simplex es una generalización del triángulo a cualquier dimensión .

Definición

En geometría , un simplex o n- simplex es el análogo n- dimensional del triángulo. Debe su nombre a que es el objeto geométrico cerrado “más simple” que tiene n dimensiones. Por ejemplo, en una línea (1 dimensión) el objeto unidimensional más simple es el segmento , mientras que en el plano (2 dimensiones) el objeto geométrico cerrado bidimensional más simple es el triángulo, y en el espacio (3 dimensiones) el objeto cerrado más simple El objeto geométrico en 3 dimensiones es el tetraedro (pirámide con base triangular).

Más exactamente, un símplex es la envolvente convexa de un conjunto de ( n +1) puntos utilizados para formar un sistema de coordenadas afines en un espacio afín de dimensión n , lo que significa que:

en una línea la referencia se hará de un origen y 1 punto (generalmente una referencia (O, I) , que define la unidad del eje), y [OI] es un segmento .
en el plano se hará la referencia de un origen y 2 puntos (generalmente una referencia (O, I, J) , definiendo la unidad para cada eje), y OIJ es un triángulo .
en el espacio el sistema de coordenadas estará formado por un origen y 3 puntos (generalmente un sistema de coordenadas (O, I, J, K) , definiendo la unidad para cada eje), y OIJK es un tetraedro .

Las coordenadas de los vértices del símplex (en el sistema de coordenadas formado por sus vértices) son entonces:

e 0 = (0, 0, 0,…, 0), e 1 = (1, 0, 0,…, 0), e 2 = (0, 1, 0,…, 0),

\ vdots

e n = (0, 0, 0,…, 1)

Sin embargo, en aras de la simetría entre los vértices, a menudo se prefiere sumergir el simplex en un hiperplano afín de espacio de dimensión n +1, atribuyendo a cada vértice las siguientes coordenadas n + 1:

e 0 = (1, 0, 0, 0,…, 0), e 1 = (0, 1, 0, 0,…, 0), e 2 = (0, 0, 1, 0,…, 0),

\ vdots

e n = (0, 0, 0, 0,…, 1)

El número n se llama dimensión o grado o incluso el orden de los n -simplex s . Por ejemplo, un 0-simplex es un punto , un 1-simplex es un segmento, un 2-simplex es un triángulo, un 3-simplex es un tetraedro, un 4-simplex es un pentacoro (o pentatopo), etc. Dado que el simplex de dimensión 0 es un singleton , al conjunto vacío a veces se le asigna la dimensión –1.

Por tanto, sea s un simplex formado por los puntos a 0 ..., a n . Un punto x de s se escribe de una manera única:

x = \ sum _ {{i = 0}} ^ {n} {t_ {i} a_ {i}}

donde t i son las coordenadas baricéntricas positivas o cero de x relativas a a 0 ..., a n . Nótese la similitud entre esta fórmula y la del equilibrio de un objeto en la mecánica estática física : que establece que la suma de las fuerzas externas aplicadas a un objeto en equilibrio es igual al vector cero. Esto se debe al hecho de que el objeto, cualquiera que sea la intensidad de estas n fuerzas que lo tiran (que se pueden representar como n resortes unidos al objeto y a los n vértices de un ( n - 1) - simplex), siempre permanecerá en este simplex: cualquier punto del simplex puede definirse por estas fuerzas que lo atraen más o menos hacia tal o cual vértice, de ahí el uso de la noción de baricentro . También se observará que, para que un objeto esté en equilibrio, necesariamente debe estar en el símplex formado por los puntos que lo atraen. ${\ Displaystyle \ sum {{\ vec {F}} _ {ext}} = {\ vec {0}}}$

Un simplex regular es un simplex que también es un politopo regular (es decir, todas sus aristas tienen la misma longitud, sus caras son de la misma naturaleza geométrica y están organizadas de la misma manera en las mismas cantidades en cada vértice).

La palabra "simplex" fue dada por Pieter Hendrik Schoute en 1902 , pero Ludwig Schläfli ya había demostrado la existencia de simplex regulares para cualquier dimensión n (por lo tanto, simplemente simplex) cuando demostró que siempre había menos tres politopos regulares para cualquier dimensión mayor. que 3 (es decir, el n- simple, así como el n - hipercubo y el n - hiperoctaedro ).

Elementos

Los elementos de un simplex se denominan n- caras , donde n es su dimensión:

Las caras 0 se llaman vértices
1-caras se llaman aristas
2 caras se llaman caras
las 3 caras se llaman celdas

Las ( n - 1) caras de un n- simple forman su envoltura .

Las n- caras de un simplex son en sí mismas símplex de dimensiones más pequeñas. Por ejemplo, un tetraedro tiene caras triangulares.

Cuando enumeramos las n- caras de los simples así como su número, obtenemos un triángulo de Pascal :

Simplex	Número de vértices	Numero de aristas	Numero de caras	Número de celdas	Número de 4 lados	Número de 5 lados	Número de 6 lados
Punto	1	-	-	-	-	-	-
Segmento	2	1	-	-	-	-	-
Triángulo	3	3	1	-	-	-	-
Tetraedro	4	6	4	1	-	-	-
Pentacoro	5	10	10	5	1	-	-
5 simplex	6	15	20	15	6	1	-
6 simplex	7	21	35	35	21	7	1
...

El triángulo de Pascal, una de cuyas características es que la segunda columna corresponde a cada número triangular , la tercera a cada número tetraédrico , la cuarta a cada número pentatópico ...

El número de vértices de un n- simplex es igual , y el número de n- caras es siempre válido porque es el símplex en sí. El número de bordes de un n -simplex vale la pena , porque se trata el número de pares de diferentes vértices que se puede lograr. ${\ Displaystyle N_ {0} = n + 1}$ ${\ Displaystyle N_ {n} = 1}$ ${\ Displaystyle N_ {1} = {\ frac {n (n + 1)} {2}}}$

Entre los números de cada elemento de un símplex, existe una relación de Euler en la que, sumando los elementos de dimensión par (vértices, caras, 4 caras, 6 caras ...) y restando los elementos de dimensión impar (aristas, celdas, 5 caras, 7 caras ...), obtenemos la característica de Euler-Poincaré del símplex, que es igual a 0 para símplex de grado par y 2 para símplex de grado impar:

${\ Displaystyle \ sum _ {i = 0} ^ {n-1} N_ {i} \ times (-1) ^ {i} = N_ {0} -N_ {1} + N_ {2} -N_ {3 } + ... + N_ {n-1} (- 1) ^ {n-1} = 1 - (- 1) ^ {n}}$ , donde es el número de ( n - 1) -faces (usamos n - 1 en la fórmula en lugar de n para no contar el n -simplex en sí y detenernos en sus elementos estrictos). $N _ {{n-1}}$

Para el segmento: 2 puntos = 2
Para el triángulo: 3 puntos - 3 aristas = 0
Para el tetraedro: 4 puntos - 6 aristas + 4 caras = 2
Para el pentacoro: 5 puntos - 10 aristas + 10 caras - 5 celdas = 0

Representaciones

Dado que los n- simples a menudo tienen más dimensiones que los objetos que estamos acostumbrados a ver en la vida cotidiana, utilizamos diferentes medios de representación para trabajar con ellos con mayor facilidad. Entre estas representaciones, a menudo usamos las proyecciones de un n- simple en un espacio dimensional inferior (generalmente 2 o 3).

Es imposible representar perfectamente un objeto en un espacio que tiene menos dimensiones que él, por lo que debemos usar estas representaciones con precaución, algunas distorsionan las longitudes, ángulos, incluso la estructura del símplex, o bien nos hacen ver segmentos que se cruzan cuando en realidad, no se cruzan.

Gráficos

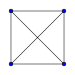
La representación bidimensional de un n- simple es un gráfico completo . Para dibujar la gráfica de un n- simple, basta con conectar todos ellos n + 1 puntos.

Cuando se trata de la gráfica de un simplex cuyo grado desconocemos, basta con contar el número de segmentos que están conectados a un vértice.

Para pasar de la gráfica de un n -simplex a la de un ( n + 1) -simplex, agregamos un nuevo punto y conectamos todos los demás a él.

Gráficos de los primeros símplex

Simplex	Segmento	Triángulo	Tetraedro	Pentatopo	5 simplex	6 simplex	7 simplex
Dimensión	1	2	3	4	5	6	7
Vértices	2	3	4	5	6	7	8
Grafico

Precaución: siendo el gráfico solo una proyección de los n -simplex en un plano, como una sombra , no se respetan las longitudes y los ángulos: es necesario imaginar que todos los segmentos son de la misma longitud, y que todos los triángulos que conectan 3 vértices son equiláteros si el simplex es regular. Además, las diagonales del gráfico nunca se encuentran en realidad, sino que pasan por delante o por detrás de las demás.

Un gráfico como estos también se llama polígono de Petrie porque se obtiene mediante la proyección ortogonal de un politopo en un plano.

Diagrama de Coxeter-Dynkin

El diagrama de Coxeter-Dynkin de un n- simple tiene la forma: … , con n círculos (llamados nodos ) en la cadena.

Símbolo de Schläfli

El símbolo de Schläfli de un n -simplex es {3,3,3, ..., 3,3}, con n - 1 por el número 3.

Propiedades

Cualquier k -simplex generado por un subconjunto de { a 0 , a 1 ,…, a n } (que son los vértices de los simplex s ) se llama k -face de s .
El conjunto de caras de s diferentes de s se llama caras propias de s , y su unión se llama arista de s .
Un n- simple no tiene diagonales porque, por definición, los n + 1 vértices de un n- simple ya están conectados entre sí.
El isobaricentro de un n- simple se encuentra en los centros de sus ( n - 1) caras. Por ejemplo, el isobaricentro de un segmento está ubicado en 1/2 de sus extremos, el isobaricentro de un triángulo equilátero está ubicado en 1/3 de los puntos medios de sus lados, el isobaricentro de un tetraedro está ubicado en 1/4 de los centros de las caras ... ${\ Displaystyle {\ frac {1} {n + 1}}}$
Un simplex es su propio dual , lo que significa que cuando conectamos todos los centros de las ( n - 1) caras de un n -simplex, recurrimos al mismo simplex, reducido a la mitad.
Si un simplex tiene una "esquina derecha" (es decir que todos los bordes que se encuentran en un vértice son perpendiculares en ellos), entonces podemos usar la generalización n- dimensional del teorema de Pitágoras : "La suma de cuadrados de ( n –1) -volúmenes de hiperfaces adyacentes a la esquina derecha es igual al cuadrado de ( n –1) -volumen opuesto a la esquina derecha ”. Por ejemplo, en un triángulo ABC en ángulo recto en A tenemos , en una pirámide ABCD en ángulo recto en A tenemos , y en un pentatopo ABCDE en ángulo recto en A tenemos . $BC ^ {2} = AB ^ {2} + AC ^ {2}$ $BCD ^ {2} = ABC ^ {2} + ABD ^ {2} + ACD ^ {2}$ $BCDE ^ {2} = ABCD ^ {2} + ABCE ^ {2} + ABDE ^ {2} + ACDE ^ {2}$
Topológicamente , un n- simple es homeomórfico a una n -esfera. Cada n- simple es un colector convexo sin agujeros de dimensión n . La característica de Euler de cualquier n- simple vale por lo tanto 0 si n es par y 2 si n es impar, como para la n -esfera.
El grupo de isometrías del n- simple regular es el grupo simétrico S n + 1 .

Longitudes y volumen notables del n -simplex regular

La altura del n -simplex regular de la arista $a$ es: ${\ Displaystyle h_ {n} = a {\ sqrt {\ frac {n + 1} {2n}}}}$ ;
el radio de la hiperesfera circunscrita es: ${\ Displaystyle R_ {n} = a {\ sqrt {\ frac {2n} {n + 1}}}}$ ;
el radio de la hiperesfera inscrita es: $r_n = \ frac a {\ sqrt {2n (n + 1)}}$ .

Demostración

${\ Displaystyle h_ {n} = R_ {n} + r_ {n}}$ .
$h_ {n} ^ {2} + R _ {{n-1}} ^ {2} = a ^ {2}$ porque la altura es perpendicular a cualquier línea recta de la base ( n - 1), por lo tanto también al radio de la esfera ( n - 1) circunscrita por la base ( n - 1), y el borde de longitud a conecta la parte superior de la altura con la parte superior de la base, los tres forman un triángulo rectángulo, simplemente aplicamos el teorema de Pitágoras .
$R_ {n} ^ {2} = r_ {n} ^ {2} + R _ {{n-1}} ^ {2}$ debido a que el radio de la n- esfera circunscrita conecta el centro de la n -esfera con un vértice, el radio de la esfera inscrita conecta el centro de la n -esfera con el centro de la base (ya que la n -esfera inscrita es tangente al n - simplex este radio es perpendicular a la base), y el radio de la ( n - 1) -esfera circunscrita en la base conecta el centro de la base a un vértice del n -simplex, todavía aplicamos el Pitágoras teorema.

Por inducción, de , obtenemos las fórmulas anunciadas. ${\ Displaystyle R_ {1} = a}$

Cada símplex tiene un hipervolumen que corresponde a su interior (para el segmento es su longitud , para el triángulo de su área , para el tetraedro de su volumen ). El n -volumen de un n -simplex es el producto de una altura (distancia entre un vértice y el centro de la cara opuesta ( n - 1)) y la base correspondiente (( n - 1) -volumen de este ( n - 1) -face), dividido por la dimensión del símplex.
Si denotamos por $V n$ el n -volumen del n -simplex regular de la arista $a$ , por lo tanto tenemos:

{\ Displaystyle V_ {n} = {\ frac {h_ {n} V_ {n-1}} {n}}}

Por inducción, a partir de la longitud de un segmento ( ) y la expresión anterior para , deducimos: $V_ {1} = a$ $h_ {n}$

V_ {n} = {\ frac {a ^ {n}} {n!}} \ Times {\ sqrt {\ frac {n + 1} {2 ^ {n}}}}

. Ejemplos:

el área del triángulo equilátero es :; ${\ Displaystyle V_ {2} = {\ frac {a ^ {2} {\ sqrt {3}}} {4}} \ approx a ^ {2} \ times 0 {,} 433}$
el volumen del tetraedro regular es: ; ${\ Displaystyle V_ {3} = {\ frac {a ^ {3} {\ sqrt {2}}} {12}} \ approx a ^ {3} \ times 0 {,} 118}$
hipervolumen la pentachore regular es: . ${\ displaystyle V_ {4} = {\ frac {a ^ {4} {\ sqrt {5}}} {96}} \ approx a ^ {4} \ times 0 {,} 023}$