Suite logística

En matemáticas , una secuencia logística es una secuencia simple, pero cuya recurrencia no es lineal. Su relación de recurrencia es

Xno+1=μXno(1-Xno), X0∈[0;1].{\ Displaystyle x_ {n + 1} = \ mu x_ {n} (1-x_ {n}), ~ x_ {0} \ in [0; 1].}

Dependiendo del valor del parámetro μ (en [0; 4] para asegurar que x permanece en [0; 1]), genera una secuencia convergente, una secuencia sometida a oscilaciones o una secuencia caótica .

A menudo citada como un ejemplo de la complejidad conductual que puede surgir de una simple relación no lineal, esta secuela fue popularizada por el biólogo Robert May en 1976 . Una aplicación del paquete de logística es modelar el tamaño de una población biológica a lo largo de generaciones.

Es la solución en tiempo discreto del modelo Verhulst . El término "logística" proviene del trabajo de Pierre François Verhulst, quien llama a la curva logística la solución de tiempo continuo de su modelo. Escribió en 1845 en su obra dedicada a este fenómeno: "Daremos el término logística a esta curva" . El autor no explica su elección, pero "logística" tiene la misma raíz que logaritmo y logistikos significa "cálculo" en griego.

Comportamiento según μ

En el modelo logístico, consideraremos que la variable anotada aquí x n designa la relación entre la población de una especie y la población máxima de esta especie (es un número entre 0 y 1). Variando el parámetro μ , se observan varios comportamientos diferentes:

Caso 0 ≤ µ ≤ 1 la población se extingue.

Finalmente, la especie morirá, independientemente de la población inicial. Es decir . lim+∞Xno=0{\ Displaystyle \ lim _ {+ \ infty} x_ {n} = 0}

Caso 1 ≤ µ ≤ 3 el tamaño de la población se estabiliza.

• Si 1 ≤ µ ≤ 2 , la población termina estabilizándose alrededor del valor , sea cual sea la población inicial. En otras palabras .μ-1μ{\ Displaystyle {\ frac {\ mu -1} {\ mu}}}lim+∞Xno=μ-1μ{\ Displaystyle \ lim _ {+ \ infty} x_ {n} = {\ frac {\ mu -1} {\ mu}}}
• Si 2 ≤ µ ≤ 3 , también termina estabilizándose después de haber oscilado durante algún tiempo. La velocidad de convergencia es lineal, excepto para µ = 3 donde es muy lenta.μ-1μ{\ Displaystyle {\ frac {\ mu -1} {\ mu}}}

Caso 3 ≤ µ ≤ 3,57 el tamaño de la población oscila entre 2, 4, 8… valores (potencia de 2).

• Si 3 <µ ≤ 1 + √6 (alrededor de 3,45), termina oscilando entre dos valores, dependiendo de µ pero no de la población inicial.
• Si 3,45 <µ <3,54 (aproximadamente), termina oscilando entre cuatro valores, de nuevo dependiente de µ pero no de la población inicial.
• Si µ es ligeramente mayor que 3,54, la población termina oscilando entre ocho valores, luego 16, 32, etc. El intervalo de valores de µ que conduce al mismo número de oscilaciones disminuye rápidamente. La relación entre dos de estos intervalos consecutivos se aproxima cada vez a la constante de Feigenbaum , δ = 4.669…. Ninguno de estos comportamientos depende de la población inicial.

Caso 3.57 ≤ µ el tamaño de la población es caótico , con algunas excepciones.

• Alrededor de µ = 3,57 , se instala el caos . Aún no se ve ninguna oscilación y ligeras variaciones en la población inicial conducen a resultados radicalmente diferentes.
• La mayoría de los valores por encima de 3,57 exhiben un carácter caótico, pero hay algunos valores aislados de µ con un comportamiento que no lo es. Por ejemplo, de 1 + √8 (aproximadamente 3,82), un pequeño intervalo de valores de µ exhibe una oscilación entre tres valores y para µ un poco mayor, entre seis valores, luego doce, y así sucesivamente. Otros intervalos ofrecen oscilaciones entre 5 valores, etc. Todos los períodos de oscilación están presentes, nuevamente independientemente de la población inicial.
• Más allá de µ = 4 , la relación entre la población de la especie y la población máxima sale del intervalo [0,1] y diverge casi para todos los valores iniciales.

Los períodos de oscilación descritos anteriormente cumplen la siguiente regla. Considere el orden de Charkovski definido en enteros estrictamente positivos de la siguiente manera:

3◃5◃7◃...◃2×3◃2×5◃2×7◃...◃2no×3◃2no×5◃2no×7◃...{\ Displaystyle 3 \; \ triangleleft \; 5 \; \ triangleleft \; 7 \; \ triangleleft \; \ ldots \; \ triangleleft \; 2 \ times 3 \; \ triangleleft \; 2 \ times 5 \; \ triangleleft \; 2 \ times 7 \; \ triangleleft \; \ ldots \; \ triangleleft \; 2 ^ {n} \ times 3 \; \ triangleleft \; 2 ^ {n} \ times 5 \; \ triangleleft \; 2 ^ {n} \ times 7 \; \ triangleleft \; \ ldots} ◃2no+1×3◃2no+1×5◃...◃2no◃2no-1◃...◃22◃2◃1{\ Displaystyle \; \ triangleleft \; 2 ^ {n + 1} \ times 3 \; \ triangleleft \; 2 ^ {n + 1} \ times 5 \; \ triangleleft \; \ ldots \; \ triangleleft \; 2 ^ {n} \; \ triangleleft \; 2 ^ {n-1} \; \ triangleleft \; \ ldots \; \ triangleleft \; 2 ^ {2} \; \ triangleleft \; 2 \; \ triangleleft \; 1 } En otras palabras, primero colocamos los impares empezando por 3 en orden ascendente, luego los impares multiplicados por 2, luego por 4, etc. y terminamos con las potencias de 2 en orden decreciente. Si un valor del parámetro µ corresponde a un período de oscilación n , entonces todos los enteros que siguen a n en el orden de Charkovski corresponden a períodos de oscilación que ya han aparecido para valores del parámetro menores que µ . Así, dado que µ = 3,82 corresponde a un período 3, ya han aparecido todos los posibles períodos de oscilación para valores de µ entre 0 y 3,82.

Un diagrama de bifurcación  (en) utilizado para resumir gráficamente los diferentes casos:

Comentarios

Algunos argumentos simples y algunos gráficos nos permiten arrojar luz parcialmente sobre los resultados anteriores.

Gráficos

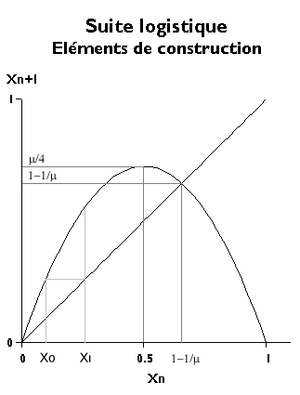
La evolución de la secuencia logística se puede representar en el plano ( x n , x n +1 ).

La ecuación básica representa una parábola que pasa por los puntos de abscisas 0 y 1 en el eje horizontal. Para que los valores de x n +1 no se vuelvan negativos, es necesario retener solo el arco incluido entre estos dos puntos; esto presenta, para x n = 1 ⁄ 2 , un máximo de valor μ ⁄ 4 . Este valor también debe estar entre 0 y 1, por lo tanto μ <4.

Si la secuencia converge, su límite satisface la ecuación lim x n +1 = lim x n . Este posible límite, denotado por x , es la solución de la ecuación cuadrática

X=μX(1-X){\ Displaystyle x = \ mu x (1-x)}

y por lo tanto puede tomar uno u otro de los valores

X=0,X=1-1/μ{\ Displaystyle x = 0, x = {1- {1 / \ mu}}}

Para describir el comportamiento de la secuencia, es necesario partir de una abscisa x 0 , determinar en la parábola el valor x 1 que luego se transforma en una nueva abscisa pasando por la bisectriz x n +1 = x n y repetir estos dos operaciones.

Áreas de convergencia

Para ciertos valores del parámetro μ, la secuencia se comporta como una secuencia clásica y converge hacia uno de los dos límites posibles. La ecuación básica se puede reescribir en la forma

Xno+1Xno=μ(1-Xno){\ Displaystyle {x_ {n + 1} \ over x_ {n}} = \ mu (1-x_ {n})}

Si , la secuencia está limitada por una secuencia geométrica que tiende hacia 0. 0≤μ≤1{\ Displaystyle 0 \ leq \ mu \ leq 1}

Para ver el comportamiento respecto al segundo límite posible, basta con realizar el cambio de variable x n = u n + 1 - 1 / μ. La fórmula se convierte en:

tuno+1+1-1/μtuno+1-1/μ=1-μtuno{\ Displaystyle {{u_ {n + 1} + 1-1 / \ mu} \ over {u_ {n} + 1-1 / \ mu}} = 1- \ mu u_ {n}}

En este caso, la condición de convergencia requiere que el segundo miembro está entre -1 y + 1: . 1≤μ≤3{\ Displaystyle 1 \ leq \ mu \ leq 3}

Comprobamos que, si u n está cerca del límite 1 - 1 / μ, entonces 1-μ u n está cerca de 2 - μ y u n tiende hacia su límite aumentando los valores si μ es menor que 2, por valores alternos si es mayor que 2.

Bifurcaciones

En el párrafo anterior, la fórmula de recurrencia de la forma x n +1 = f ( x n ) permitió obtener los primeros atractores buscando un posible límite conforme a la ecuación x = f ( x ).

Cuando μ se vuelve mayor que 3, debemos encontrar una solución a la ecuación x = f ( f ( x )). Esto conduce a una ecuación de cuarto grado que, naturalmente, tiene las raíces ya conocidas , pero ya no son atractoras, y el par de nuevas raíces. 0,1-1μ{\ Displaystyle 0,1 - {\ frac {1} {\ mu}}}

12(1+μμ±1μμ2-2μ-3){\ Displaystyle {1 \ over 2} \ left ({1+ \ mu \ over \ mu} \ pm {1 \ over \ mu} {\ sqrt {\ mu ^ {2} -2 \ mu -3}} \ derecho)}

No hay más convergencia: aparece un ciclo límite. El resultado de la iteración cambia alternativamente de una de las dos últimas raíces a la otra: u n + 1 = u n-1 mientras que u n + 2 = u n . Para μ = 3.4, aparecen los sucesivos valores aproximados 0.84, 0.45, 0.84, 0.45, 0.84 ....

Más allá del límite de estabilidad de este ciclo, √6 + 1, se producen dos nuevas bifurcaciones, que dependen de las soluciones de x = f (f (f (f (x)))). Para μ = 3.47, los valores sucesivos son del orden de 0.47, 0.86, 0.40, 0.84, 0.47 ...

Caos

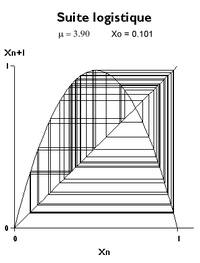
De la bifurcación a la bifurcación, las evoluciones se vuelven cada vez más complejas. El proceso da como resultado, aproximadamente μ> 3,57, en sistemas que generalmente ya no presentan atractores visibles. Los gráficos representan entonces una evolución "caótica" en el sentido habitual del término.

Sin embargo, en el lenguaje de los matemáticos, la palabra caos representa una fuerte sensibilidad a las condiciones iniciales. Las dos gráficas correspondientes a μ = 3.9 con valores iniciales u 0 0.100 y 0.101 muestran que las trayectorias se alejan una de la otra hasta que rápidamente se vuelven distintas. En un problema concreto, las condiciones iniciales nunca se conocen con exactitud: después de cierto tiempo, un fenómeno caótico se ha vuelto impredecible aunque la ley que lo define sea perfectamente determinista.

Apéndices

Bibliografía

• Alain Hillion , Las teorías matemáticas de las poblaciones , París, Presses Universitaires de France , coll.  "  ¿Qué sé yo?  "1986, 127  p. , n ° 2258 ( ISBN  2-13-039193-1 )
• Nicolas Bacaër , Historias de matemáticas y poblaciones , París, Éditions Cassini, coll.  "Sal y hierro",2008, 212  p. ( ISBN  978-2-84225-101-7 , aviso BnF n o  FRBNF42035729 ) , "Verhulst y la ecuación logística"

Artículos relacionados

• Sistema dinámico
• Teoría del caos
• Teoría ergódica
• Fractal de Lyapunov
• Retroalimentación , autorregulación

enlaces externos

• (es) Elmer G. Wiens, El mapa logístico y el caos
• [PDF] Daniel Perrin, La suite logística y el caos
• (fr) Experiencia digital interactiva del diagrama de bifurcación de la aplicación logística http://experiences.math.cnrs.fr

Notas y referencias

1. (in) RM May , "  Modelos matemáticos simples con dinámicas muy complicadas  " , Nature , vol.  261, n o  55601976, p.  459–467 ( DOI  10.1038 / 261459a0 )
2. (in) ¿Por qué no la curva logística autocatalítica y de ojiva?