Cono (geometría)

En geometría , un cono es una superficie reglada o un sólido .

Área

Caso general

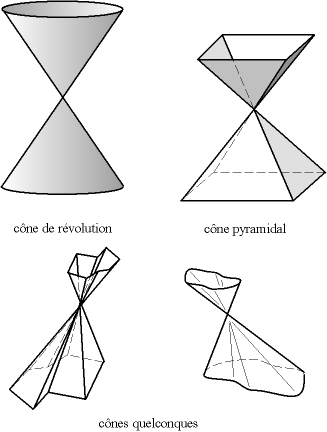
Un cono es una superficie reglada definida por una línea recta ( d ), denominada generatriz , que pasa por un punto fijo S llamado vértice y un punto variable que describe una curva ( c ), llamado dirigir curva .

También hablamos en este caso de superficie cónica .

Cono de revolución

Entre estas superficies cónicas, la más estudiada es el cono de revolución en el que la curva directriz es un círculo con centro O ubicado en un plano perpendicular a (SO). Este cono se llama de revolución porque se puede generar simplemente por la rotación de una línea (d) que pasa por S alrededor de un eje (Sz) diferente de (d). El generador del cono forma un ángulo fijo con el eje de rotación. α{\ Displaystyle \ alpha}

Es a partir de este cono de revolución que los matemáticos (incluido Apolonio de Perga ) han clasificado un conjunto de curvas como cónicas (intersección del cono y un plano): círculos , elipses , parábolas , hipérbolas .

En el sistema de coordenadas ortonormal ( S , i , j , k ), la ecuación del cono de revolución con eje ( Sz ) y vértice S viene dada por:

X2+y2=z2(broncearse⁡ α)2{\ Displaystyle x ^ {2} + y ^ {2} = z ^ {2} (\ tan \ \ alpha) ^ {2}}

donde es el ángulo del cono (o medio ángulo en la parte superior), formado por el eje de revolución y un generador. α{\ Displaystyle \ alpha}

Secciones de un cono de revolución por un plano

En los casos en que el plano sea paralelo o perpendicular al eje de revolución del cono, se obtienen las siguientes curvas:

• La sección de un cono de revolución por un plano perpendicular al eje de revolución es un círculo.
• La sección de un cono de revolución por un plano paralelo al eje de revolución es
  • la unión de dos rectas secantes si el plano contiene el eje de revolución
  • una hipérbola en el caso contrario

De manera más general, la sección de un cono de revolución por un plano da una cónica . Entonces encontramos

• una parábola (posiblemente reducida a un generador) cuando el plano es estrictamente paralelo a un generador del cono
• una elipse (posiblemente reducida a un punto) cuando el ángulo formado por el vector normal al plano y el eje de rotación es menor que π / 2 - α
• una hipérbola (posiblemente reducida a dos líneas secantes) cuando el ángulo formado por el vector normal al plano y el eje de rotación es mayor que π / 2 - α

Sólido

Caso general

También se llama cono al sólido delimitado por la superficie cónica, el vértice S y un plano ( P ) que no contiene S y secante a todas las generatrices. La sección del plano y la superficie se llama base del cono.

Cuando la sección es circular con centro O y la línea ( OS ) es perpendicular a la sección, el cono se llama cono de revolución o cono circular recto . Es el cono más famoso ( cono de helado , sombrero de payaso ). En este caso, la distancia entre el vértice de cualquier punto del círculo es constante y se denomina apotema del cono.

Cuando la curva cerrada es un polígono , obtenemos una pirámide .

Volumen

Cualquiera que sea la forma del cono, su volumen es siempre un tercio del volumen de un cilindro con la misma base y altura:

V=13B×h{\ Displaystyle V = {\ frac {1} {3}} B \ times h}

donde B es el área de la base y h es la altura del cono, es decir, la distancia entre el vértice S y el plano ( P ).

Demostración

Utilicemos que las dimensiones de una sección plana paralela a la base aumentan linealmente desde el vértice S hacia la base. La sección plana, a cualquier distancia y de S , es la base escalada por un factor de y / h , donde h es la distancia entre S y la base. Dado que el área de cualquier forma se multiplica por el cuadrado de la forma escalada, el área de la sección plana a una distancia y de S es By 2 / h 2 .

El volumen viene dado por la integral

Bh2∫0hy2Dy=Bh2[y33]0h=Bh3.{\ Displaystyle {\ frac {B} {h ^ {2}}} \ int _ {0} ^ {h} y ^ {2} {\ rm {d}} y = {\ frac {B} {h ^ {2}}} \ left [{\ frac {y ^ {3}} {3}} \ right] _ {0} ^ {h} = {\ frac {Bh} {3}}.}

Cono truncado

Cuando cortamos el cono por un plano paralelo a su base, obtenemos dos sólidos. El que contiene el vértice es una reducción del cono original, el segundo sólido es un cono truncado. Su volumen se expresa en función de sus dos bases B 1 y B 2 y de su altura h (la distancia que separa las dos bases) según la fórmula: V=h3×(B1+B1B2+B2){\ Displaystyle V = {\ frac {h} {3}} \ times (B_ {1} + {\ sqrt {B_ {1} B_ {2}}} + B_ {2})}

Caso del cono de revolución

En el caso particular del cono de revolución, las fórmulas para el volumen V y el área A (área de la superficie que encierra el cono: área lateral + base circular) son

V=13πr2×h{\ Displaystyle V = {\ frac {1} {3}} \ pi r ^ {2} \ times h} A=πr(r+a){\ Displaystyle A = \ pi r (r + a) \,},

donde r es el radio del círculo base, h es la altura del cono y

a=r2+h2{\ Displaystyle a = {\ sqrt {r ^ {2} + h ^ {2}}}}

la apotema del cono.

Área lateral

El área lateral A l (sin la base) es

Al=πrr2+h2=πr21+h2r2{\ Displaystyle A_ {l} = \ pi r {\ sqrt {r ^ {2} + h ^ {2}}} = \ pi r ^ {2} {\ sqrt {1 + {\ frac {h ^ {2 }} {r ^ {2}}}}}}

ahora, de acuerdo con las relaciones trigonométricas en el triángulo rectángulo, tenemos

1+h2r2=1pecado2⁡α{\ Displaystyle 1 + {\ frac {h ^ {2}} {r ^ {2}}} = {\ frac {1} {\ sin ^ {2} \ alpha}}}

donde α es la mitad del ángulo del vértice. Si A 0 es el área de la base π⋅ r  2 , entonces tenemos

Al=A0pecado⁡α{\ Displaystyle A_ {l} = {\ frac {A_ {0}} {\ sin \ alpha}}}

Esta fórmula se utiliza por ejemplo para calcular el área del frente de la llama en el caso de una llama cónica, por lo tanto, el consumo de gas y la potencia de esta llama.

Sección del cono de revolución por un plano

Cuando cortamos un cono de revolución sólido, por un plano paralelo a la base, obtenemos un círculo. El radio r 1 de este círculo se obtiene en función del radio r de la base, la altura h del cono y la distancia h 1 entre el plano y el vértice del cono utilizando el teorema de Thales  :

rh=r1h1{\ Displaystyle {\ frac {r} {h}} = {\ frac {r_ {1}} {h_ {1}}}}

Cuando cortamos este mismo cono por un plano que contiene su eje de revolución, obtenemos un triángulo isósceles de base 2r y altura h .

Patrón o desarrollo de un cono de revolución.

Para obtener el patrón de un cono de revolución de radio r y altura h , primero debemos calcular la apotema

a=r2+h2{\ Displaystyle a = {\ sqrt {r ^ {2} + h ^ {2}}}}.

Entonces es suficiente dibujar un círculo de radio r y una porción de un círculo de radio a cuyo ángulo central es igual al ángulo completo. ra{\ Displaystyle {\ frac {r} {a}}}

Ver también

Artículos relacionados

• Proyección central
• Estereorradián

En la naturaleza

• Conodonta , una clase de pez agnath fósil, cuya etimología significa "diente" con forma de cono.

Enlace externo

A. Javary, Tratado de geometría descriptiva , 1881 (sobre Gallica ): Conos y cilindros, esfera y superficies de segundo grado

<img src="https://fr.wikipedia.org/wiki/Special:CentralAutoLogin/start?type=1x1" alt="" title="" width="1" height="1" style="border: none; position: absolute;">